SUMMARY
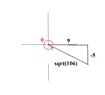
This discussion focuses on solving situational problems involving trigonometric identities, specifically calculating sine and cosine values using the Pythagorean theorem. The values derived are $\sin\theta = \frac{-5}{\sqrt{106}}$ and $\cos\theta = \frac{9}{\sqrt{106}}$. The final expression for the sum of sine and cosine is $\sin\theta + \cos\theta = \frac{4}{\sqrt{106}}$. The calculations emphasize the relationship between the sides of a right triangle and their corresponding trigonometric functions.
PREREQUISITES
- Understanding of trigonometric identities
- Knowledge of the Pythagorean theorem
- Familiarity with right triangle properties
- Basic algebra for manipulating fractions and square roots
NEXT STEPS
- Study the unit circle and its application in trigonometry
- Learn about the derivation of trigonometric identities
- Explore advanced trigonometric equations and their solutions
- Practice problems involving the application of sine and cosine in real-world scenarios
USEFUL FOR
Students learning trigonometry, educators teaching trigonometric identities, and anyone needing to solve problems involving sine and cosine in mathematical contexts.

 )
)