SUMMARY
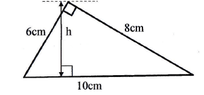
The discussion focuses on solving for the height of a triangle without using trigonometry, specifically for educational purposes. The area of the triangle is calculated using the formula area = (base * height) / 2, resulting in an area of 24 for a triangle with a base of 10. By rearranging the area formula, the height (h) is determined to be 4.8. Additionally, similarity of triangles is employed to confirm the height using ratios, yielding the same result of 4.8.
PREREQUISITES
- Understanding of basic geometry concepts, specifically triangles.
- Familiarity with the area formula for triangles: area = (base * height) / 2.
- Knowledge of triangle similarity and proportional relationships.
- Basic algebra skills for solving equations.
NEXT STEPS
- Study the properties of similar triangles and their applications.
- Explore different methods for calculating the area of triangles.
- Learn about geometric proofs involving triangle height and area.
- Investigate other non-trigonometric methods for solving geometric problems.
USEFUL FOR
Parents helping children with geometry homework, educators teaching triangle properties, and students preparing for exams in basic mathematics.