chwala
Gold Member
- 2,828
- 425
- Homework Statement
- See attached
- Relevant Equations
- Complex numbers
The problem is as shown...all steps are pretty easy to follow. I need help on the highlighted part in red. How did they come to;
##z^4+8z^2+16-9z^2=0## or is it by manipulating ##-z^2= 8z^2-9z^2?## trial and error ...
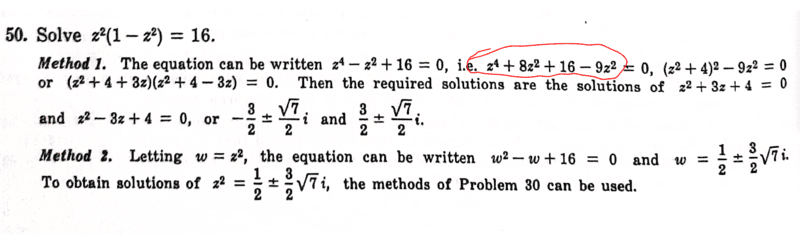
##z^4+8z^2+16-9z^2=0## or is it by manipulating ##-z^2= 8z^2-9z^2?## trial and error ...