corychu
- 2
- 7
I've tried to make an animation using python to demonstrate the 1-D simple harmonic oscillator and step potential examples. Hope that it can be useful for some of you. Have fun~ :)
https://blog.gwlab.page/solving-1-d-Schrödinger-equation-in-python-dcb3518ce454
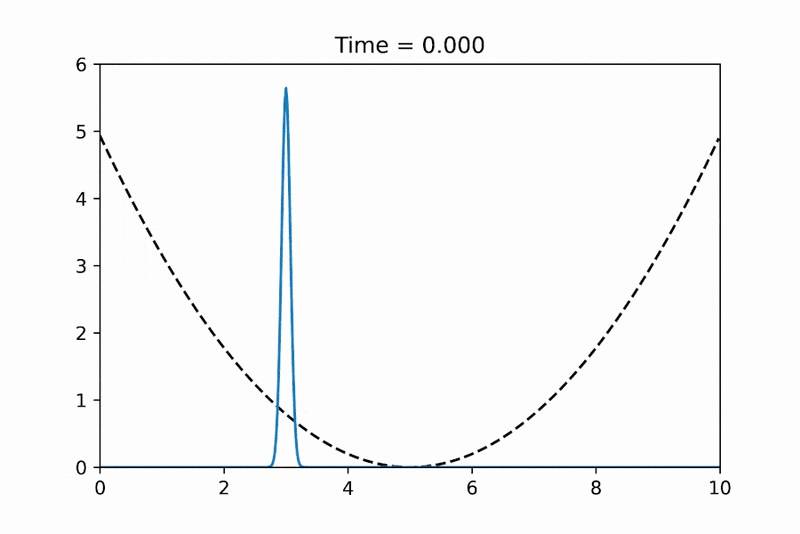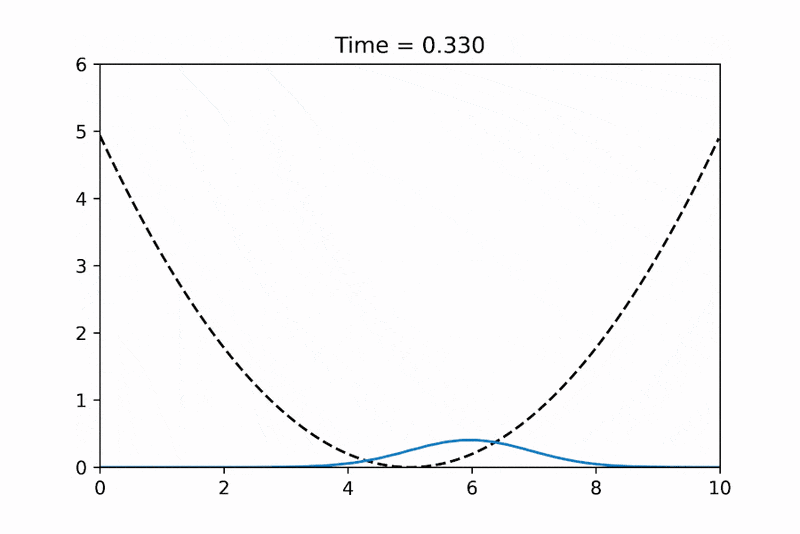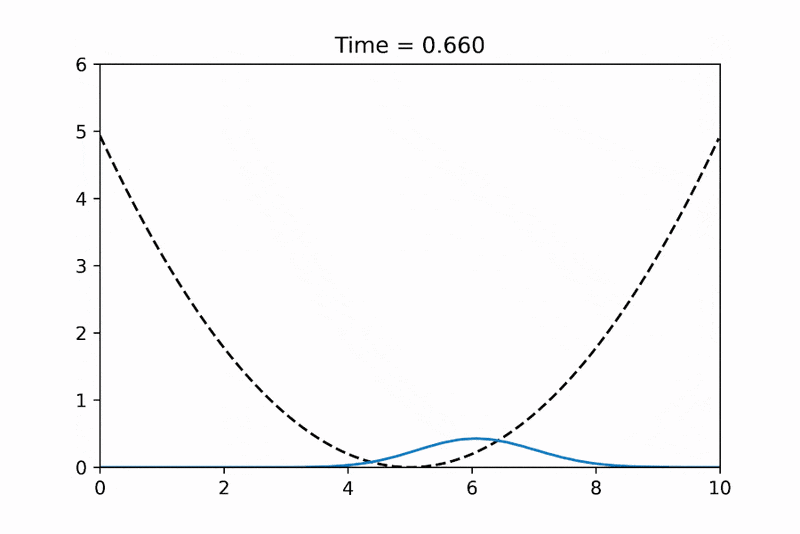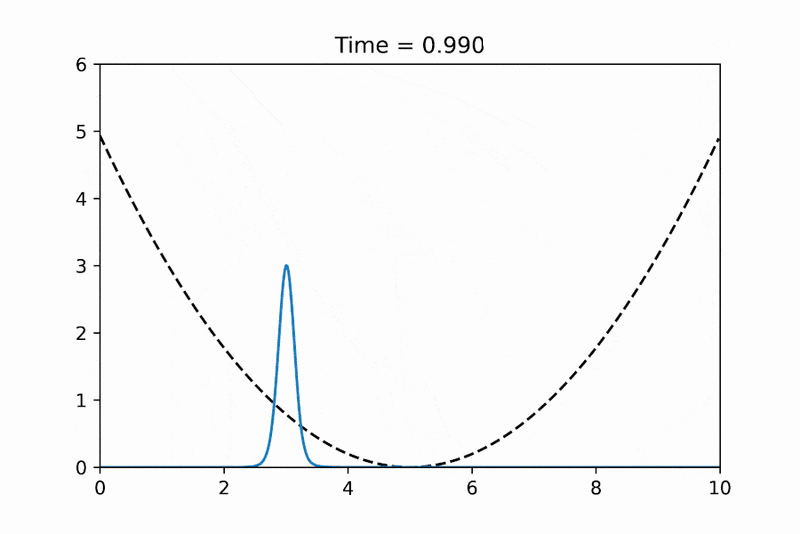
By the way, If you are interested, I also implemented a C++ version using RK4 and finite-difference scheme with Eigen library:
https://github.com/c0rychu/SchrodingerEq_1D_tutorial/tree/master/step_potential_cpp
https://blog.gwlab.page/solving-1-d-Schrödinger-equation-in-python-dcb3518ce454
By the way, If you are interested, I also implemented a C++ version using RK4 and finite-difference scheme with Eigen library:
https://github.com/c0rychu/SchrodingerEq_1D_tutorial/tree/master/step_potential_cpp
Last edited: