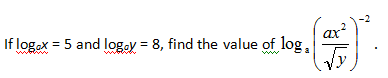Alaba27
- 18
- 0
If log[a]x=5 and log[a]y=8, solve:
log[a]((ax2)/(√y))-2
---------
I am completely lost. I've tried some ways of doing this question but I can't get past the second and third steps. This is one of the last questions in my homework and I do not have a step-by-step solutions manual, only the final answer which would be useless because I will have no idea how to get there. Can someone please give me a step-by-step solution? Please and thanks!
log[a]((ax2)/(√y))-2
---------
I am completely lost. I've tried some ways of doing this question but I can't get past the second and third steps. This is one of the last questions in my homework and I do not have a step-by-step solutions manual, only the final answer which would be useless because I will have no idea how to get there. Can someone please give me a step-by-step solution? Please and thanks!