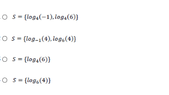Solving for an exponential equation using logarithms 16^{x}-5(4)^{x}-6=0

In summary, the conversation discusses the difficulty in solving an exponential equation and the use of logarithms to solve it. The original equation was written with an error, which was corrected to $(4^x)^2-5(4^x)-6=0$. The solution to this equation is $x=0.833215$, as shown by W|A. The conversation also mentions the use of quadratic formula to solve the equation.
  • #1
sp3
8
0
Hello I'm having trouble solving for this exponential equation : 16^{x}-(5,4)^{x}-6=0
I used some logarithms properties but can't get anything close to the following solutions here View attachment 8366
I tried using log base 16 : log16(16^{x})-6=log16((5,4)^{x}) ; then x - xlog16(5,4)=6 ;
factorizing x : x(1-log16(5,4))=6 here I get lost... I don't know how they got to log base 4 ( the answer is log4(6)) ... i thought about rewriting 5,4 as a fraction 27/5 but it doesn't help a lot... thanks in advance for the help
 

Attachments

  • solutions45.png
    solutions45.png
    5.8 KB · Views: 128
Mathematics news on Phys.org
  • #2
Are you sure you've copied the equation correctly? According to W|A, the solution to the given equation is

\(\displaystyle x=0.833215\)

But:

\(\displaystyle \log_4(6)\approx1.292481250360578\)
 
  • #3
Hi sp3, welcome to MHB! ;)

Can it be that your equation should be $16^x-5\cdot 4^x-6=0$?

If so then we can write it as $(4^x)^2-5(4^x)-6=0$ and apply the quadratic formula.
 
  • #4
Thank youu I suspected something was up with this decimal number... thanks a million times guys! :D
 

FAQ: Solving for an exponential equation using logarithms 16^{x}-5(4)^{x}-6=0

What is an exponential equation?

An exponential equation is an equation in which the variable appears in the exponent. It can be written in the form y = ab^x, where a and b are constants and x is the variable.

How do I solve for an exponential equation using logarithms?

To solve for an exponential equation using logarithms, take the logarithm of both sides of the equation. This will allow you to bring the variable out of the exponent and solve for it using algebraic methods.

What is the purpose of using logarithms in solving an exponential equation?

Logarithms allow us to solve for variables that are in the exponent, which can be difficult to solve for using traditional algebraic methods. They also allow us to convert exponential equations into linear equations, which are easier to solve.

What are the steps for solving for an exponential equation using logarithms?

The steps for solving for an exponential equation using logarithms are:

  1. Take the logarithm of both sides of the equation.
  2. Use logarithm rules to simplify the equation.
  3. Isolate the variable and solve for it using algebraic methods.
  4. If necessary, check your solution by plugging it back into the original equation.

Can I use any base for the logarithm when solving an exponential equation?

Yes, you can use any base for the logarithm when solving an exponential equation. However, it is often more convenient to use a base that is related to the numbers in the equation (such as base 10 or base e). It is important to be consistent with the base you choose throughout the entire equation.

Similar threads

MHB Rewrite in exponential form: Log(6) 1294 = 4
Replies
2
Views
2K
MHB -s6.6 solve exponential eq 3^x-14\cdot 3^{-x}=5
Replies
1
Views
850
MHB How Do I Solve a Logarithmic Equation with Different Bases and Variables?
Replies
4
Views
1K
MHB Exponential Equation solve 54⋅2^(2x)=72^x⋅√0.5
Replies
3
Views
2K
MHB Logarithmic Equation solve log_(3x)3+log_(x/3)3=5/12
Replies
1
Views
1K
MHB How can I solve more complex exponential equations?
Replies
2
Views
1K
Can I Use Logarithms to Solve Exponential Equations?
Replies
7
Views
1K
MHB Solve Exponential Equation 4^(5-9x)=1/(8^(x-2) )
Replies
7
Views
3K
MHB Solve Logarithms Problems: Find Profit & Interest Rate
Replies
3
Views
2K
MHB √(5-6*x)*ln(4*√(x)-√(a))=√(5-6*x)*ln(2*x+a)
Replies
20
Views
3K

Hot Threads

Recent Insights

Back
Top