Solving a Problem with Interchanging Field Tensors

[milkism]

Homework Statement

Expressing the field tensor in terms of the four dimensional Levi-Civita symbol and covariant dual field tensor.

Relevant Equations

See solution.

Exercise:

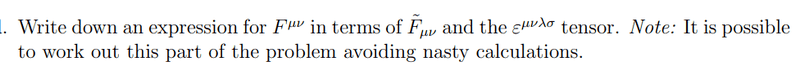
Solution:

The result is correct, but I'm unsure about equation from 29 to 30 where right-hand side became just the covariant dual field tensor. I assumed that I could interchange the covariant dual- and normal covariant field tensor, but don't think it's possible since matrices aren't commutative.
I think I bruteforced to get the correct result.

P.S: definition (20) is just the definition of the four-dimensional Levi-Civita symbol.

 

[haushofer]

You can interchange F and its dual in the conteaction. You're adding (products of) components, which commute. You don't multiply whole matrices.

Btw, you should then also worry about those implicit metric tensor "matrices" in the contraction of F with itself.

 

[milkism]

You can interchange F and its dual in the conteaction. You're adding (products of) components, which commute. You don't multiply whole matrices.

Btw, you should then also worry about those implicit metric tensor "matrices" in the contraction of F with itself.

Wow, thx!

 

[vanhees71]

Just use Appendix A.4 in

https://itp.uni-frankfurt.de/~hees/pf-faq/srt.pdf

One must be very careful concerning the sign conventions, i.e., whether you have $\epsilon^{\mu \nu \rho \sigma}$ as the usual Levi-Civita symbol and then necessarily $\epsilon_{\mu \nu \rho \sigma}=-\epsilon^{\mu \nu \rho \sigma}$ or vice versa, when using different books/papers.

 

[robphy]

From
$(29)\qquad \color{red}{\tilde{F}^{\mu \nu} \tilde{F}_{\mu \nu}} F^{\kappa \lambda}=\frac{1}{2} \epsilon^{\mu \nu \kappa \lambda} \color{blue}{F_{\kappa \lambda}} \tilde{F}_{\mu \nu} \color{blue}{F^{\kappa \lambda}}$
which can be rewritten (using tensorial methods) as
$(29)\qquad \color{red}{\tilde{F}^{\mu \nu} \tilde{F}_{\mu \nu}} F^{\kappa \lambda}=\frac{1}{2} \epsilon^{\mu \nu \kappa \lambda} \tilde{F}_{\mu \nu} \color{blue}{F_{\kappa \lambda}} \color{blue}{F^{\kappa \lambda}}$inserting
$(26)\qquad \color{red}{\tilde{F}^{\mu \nu} \tilde{F}_{\mu \nu}}=-2\left(B^2-\frac{E^2}{c^2}\right)$

$(25)\qquad \color{blue}{F_{\kappa \lambda} F^{\kappa \lambda}}=2\left(B^2-\frac{E^2}{c^2}\right)$

you get

$\color{red}{-2\left(B^2-\frac{E^2}{c^2}\right)} F^{\kappa \lambda}=\frac{1}{2} \epsilon^{\mu \nu \kappa \lambda} \tilde{F}_{\mu \nu} \ \color{blue}{2\left(B^2-\frac{E^2}{c^2}\right)}$

$\color{red}{-1} F^{\kappa \lambda}=\frac{1}{2} \epsilon^{\mu \nu \kappa \lambda} \tilde{F}_{\mu \nu}$
which is equal to "minus Eq. (30)"

 

[TSny]

From the first post we have equation (27):

Here, the Einstein summation notation is being used, so the $\kappa$ and $\lambda$ on the right side are dummy summation indices.

Then we read

If the Einstein convention is still being assumed, then all the indices appearing in (28) are dummy summation indices.

The next step in post #1 is

Here, we have confusion. The $\kappa$ and $\lambda$ indices appear alone on the left side. So, these indices are not being summed on the left side. Going from left to right on the right side of (29), we know that the first two $\kappa$'s are summation indices. But, the $\kappa$ in the last factor, $F^{\kappa \lambda}$, is not suummed since this $\kappa$ corresponds to the $\kappa$ on the left side of the equation. The same remarks can be made for the $\lambda$'s in (29).

Note that (29) can be written with less confusion as

$$\tilde{F}^{\mu \nu} \tilde{F}_{\mu \nu} F^{\kappa \lambda}= \frac 1 2 \epsilon^{\mu \nu \alpha \beta}F_{\alpha \beta} \tilde{F}_{\mu \nu} F^{\kappa \lambda} $$

Here, it is clear that $\mu$, $\nu$, $\alpha$, and $\beta$ are summation indices while the $\kappa$ and $\lambda$ are fixed indices that are not summed. However, it doesn't appear to me that this equation is very helpful in getting to the result of expressing $F^{\mu \nu}$ in terms of $\tilde{F}_{\mu \nu}$ and the Levi-Civita tensor.

A better approach is to follow @vanhees71. Start with $$\tilde{F}^{\alpha \beta} = \frac 1 2 \epsilon^{\alpha \beta \kappa \lambda}F_{\kappa \lambda} $$ Raise and lower indices to write this as $$\tilde{F}_{\alpha \beta} = \frac 1 2 \epsilon_{\alpha \beta \kappa \lambda}F^{\kappa \lambda} $$ Multiply both sides by $\epsilon^{\mu \nu \alpha \beta}$ and sum over $\alpha$ and $\beta$. $$\epsilon^{\mu \nu \alpha \beta} \tilde{F}_{\alpha \beta} = \frac 1 2 \epsilon^{\mu \nu \alpha \beta} \epsilon_{\alpha \beta \kappa \lambda}F^{\kappa \lambda} $$ Proceed by using identities (A.4.5) and (A.3.1) in the appendices of https://itp.uni-frankfurt.de/~hees/pf-faq/srt.pdf. It is helpful to note that $\epsilon_{\alpha \beta \kappa \lambda} = \epsilon_{ \kappa \lambda \alpha \beta}$.