SUMMARY
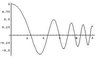
The discussion centers on solving the second order differential equation y'' + y(x^2 + e^x) = 0, which features both polynomial and transcendental functions as coefficients. Participants agree that analytical solutions are unlikely and suggest using series solutions as a viable approach. One user mentions utilizing NDSolve with initial conditions y(0)=1 and y'(0)=0, which provided a numerical solution. The consensus emphasizes the importance of understanding series methods, as they are not adequately covered in the referenced textbook.
PREREQUISITES
- Understanding of second order differential equations
- Familiarity with series solutions in differential equations
- Experience with numerical methods, specifically NDSolve
- Basic knowledge of polynomial and transcendental functions
NEXT STEPS
- Study the series method for solving differential equations
- Explore the capabilities of NDSolve in Mathematica for numerical solutions
- Read about the theory behind series solutions in elementary differential equations textbooks
- Investigate the relationship between initial conditions and solution behavior in differential equations
USEFUL FOR
Students and educators in mathematics, particularly those studying differential equations, as well as practitioners seeking numerical methods for solving complex differential equations.