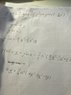Solving an ODE using shooting method

[spaghetti3451]

Hi, I am trying to solve the following ODE for my maths project:

$y'' = \frac{\alpha}{2}y^3 - \frac{3}{2}y^2 + y - \frac{3}{x} y'$

under the following boundary conditions:

$y'(0) = 0$
$y(x) \rightarrow y \_ \equiv 0\ \text{as}\ x \rightarrow \infty$
As a first step, I converted this problem into a set of coupled ODEs:

$\frac{dy}{dx} = z$
$\frac{dz}{dx} = \frac{\alpha}{2}y^3 - \frac{3}{2}y^2 + y - \frac{3}{x} z$

under the following boundary conditions:

$z(0) = 0$
$y(x) \rightarrow y \_ \equiv 0\ \text{as}\ x \rightarrow \infty$Next, my source tells me to use the shooting method to convert the BVP into an IVP, which means that I have to use two initial guesses of $y(0)$ to be able to use the secant method to find the correct value of $y(0)$.

Now, my question is, according to my source, I can avoid the singularity at x = 0 using Taylor expansion as follows:

$y(r_{0}) = y_{0} + \frac{1}{16} r_{0}^{2} (2y_{0} - 3y_{0}^{2} + \alpha y_{0}^{3})$

I see how you can estimate $y(r_{0})$ where $r_{0}$ is a tiny distance away from the origin, but I don't really see how they dervied this expression. Could anyone help me out?

 

[HomogenousCow]

Just set y(0)'=0 and y(0)=y_0 in the original DE.
Then use this as your second derivative in your taylor series.

EDIT: Tried it myself, something weird is going on. The numerical factors come out different for me.
Maybe an error? I don't see where the factor of 1/16 comes from. It comes out as 1/4 for me.

 

[Chestermiller]

Start out by representing y as a function of x at small values of y by y(x) = y(0)+bx². Then

y' = 2bx
y''=2b

3y'/x = 6b

So $8b=\frac{\alpha}{2}y(0)^3-\frac{3}{2}y(0)^2+y(0)$

So, $y(r_0)=y(0)+br_0^2=y(0)+\frac{1}{8}r_0^2(\frac{\alpha}{2}y(0)^3-\frac{3}{2}y(0)^2+y(0))$

Chet

 

[spaghetti3451]

Thanks for the solution. I also came to the conclusion, but I used $\frac{y''(0)}{2}$ in place of $b$. I have written the code that solves the ODE in my original post, but it's giving me unexpected results. I was wondering if anyone in Physics Forums might want to have a look at it.

 

[blue_raver22]

Hello,

I can provide some insight into this problem. The shooting method is a numerical technique used to solve boundary value problems (BVPs) by converting them into initial value problems (IVPs). This involves using two initial guesses for the boundary condition at the starting point, and then using the secant method to find the correct value of the boundary condition.

In your case, the BVP has been converted into a set of coupled ODEs, which is a common approach. However, you have also encountered a singularity at x=0, which can be problematic for numerical methods. The Taylor expansion you mentioned is a way to avoid this singularity by approximating the solution near x=0 using the values at a small distance away (r0).

To understand how this expression was derived, we can consider the Taylor series expansion of y(x) around x=0:

$y(x) = y(0) + y'(0)x + \frac{y''(0)}{2!}x^2 + ...$

Since we know y'(0) = 0 from the boundary condition, we can simplify this to:

$y(x) = y(0) + \frac{y''(0)}{2!}x^2 + ...$

Now, if we expand y''(0) using the given ODE, we get:

$y''(0) = \frac{\alpha}{2}y(0)^3 - \frac{3}{2}y(0)^2 + y(0) - \frac{3}{x}y'(0)$

Substituting y'(0)=0 and rearranging, we get:

$y(0) = \frac{y''(0)}{\frac{\alpha}{2}y(0)^2 - \frac{3}{2}y(0) + 1}$

Finally, using the definition of r0 as a small distance away from x=0, we can write:

$y(r0) = y(0) + y'(0)r0 + \frac{y''(0)}{2!}r0^2 + ...$

Substituting y'(0)=0 and y''(0) from the previous expression, we get:

## y(r0) = y(0) + \frac{y''(0)}{2!}r