- #1
hnicholls
- 49
- 1
I have the following non-stationary state of the QSHO:
Ψ =
[
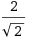
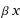
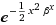e −3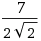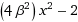iωt/2 +
[
]
e −5iωt/2]
where β = mω/ħ
in calculating <E2>
The answer I see in the textbook is 6.17 ħ2ω2.
This answer suggests that in calculating <E2> = ∫ Ψ*Ĥ2Ψ dx
where Ψ is composed of the above two terms Ψ1 and Ψ2 (a linear combination of E1 and E2 of the QSHO) the cross terms need to be zero to eliminate the time dependence as reflected in the answer in the textbook.
This leaves us with the inside and outside terms
∫ Ψ1*Ĥ2Ψ1 dx + ∫ Ψ2*Ĥ2Ψ2 dx and calculating the sum of these inside and outside terms producing the answer in the textbook.
However, as I calculated the cross terms ∫ Ψ1*Ĥ2Ψ2 dx is zero as it is an odd function, but ∫ Ψ2*Ĥ2Ψ1 dx is not zero as it is an even function. This would not eliminate the time dependence and would not result in a non oscillating result as reflected in the textbook.
Am I missing something here?
Ψ =
where β = mω/ħ
in calculating <E2>
The answer I see in the textbook is 6.17 ħ2ω2.
This answer suggests that in calculating <E2> = ∫ Ψ*Ĥ2Ψ dx
where Ψ is composed of the above two terms Ψ1 and Ψ2 (a linear combination of E1 and E2 of the QSHO) the cross terms need to be zero to eliminate the time dependence as reflected in the answer in the textbook.
This leaves us with the inside and outside terms
∫ Ψ1*Ĥ2Ψ1 dx + ∫ Ψ2*Ĥ2Ψ2 dx and calculating the sum of these inside and outside terms producing the answer in the textbook.
However, as I calculated the cross terms ∫ Ψ1*Ĥ2Ψ2 dx is zero as it is an odd function, but ∫ Ψ2*Ĥ2Ψ1 dx is not zero as it is an even function. This would not eliminate the time dependence and would not result in a non oscillating result as reflected in the textbook.
Am I missing something here?
