- #1
zenterix
- 480
- 70
- Homework Statement
- Find the general solution to the differential equation
- Relevant Equations
- ##y''+2y'+y=\frac{e^{-x}}{x^2}##
The characteristic equation has a zero discriminant and the sole root of ##-1##.
The general solution to the associated homogeneous equation is thus
$$y_h(x)=e^{-x}(c_1+c_2x)\tag{1}$$
Now we only need to find one particular solution of the non-homogeneous equation.
The righthand side of the non-homogeneous equation, call it ##R(x)##, is not a polynomial, nor does it fall in the category of ##p(x)e^{mx}## with ##p## being a polynomial. These are perhaps the two easiest special cases of ##R(x)## to solve because they can be solved by the method of undetermined coefficients.
##R(x)## is also not an exponential multiplied by an expression containing ##\sin## and/or ##\cos##, which can also be solved by the method of undetermined coefficients.
Thus, I have chosen to solve using a more general method based on the following theorem in Apostol's Calculus, Volume I

We have ##v_1(x)=1## and ##v_2(x)=x## as our solutions to ##L(y)=0##, ie the homogeneous equation.
The Wronskian of ##v_1## and ##v_2## is
$$W(x)=
\begin{vmatrix}
1 & 0\\
x & 1
\end{vmatrix}=1
\tag{2}$$
Thus,
$$t_1(x)=-\int x\cdot\frac{e^{-x}}{x^2}dx=\int\frac{e^{-x}}{x}dx\tag{3}$$
$$t_2(x)=\int \frac{e^{-x}}{x^2}dx\tag{4}$$
How do we solve these integrals?
Math software doesn't get me very far:
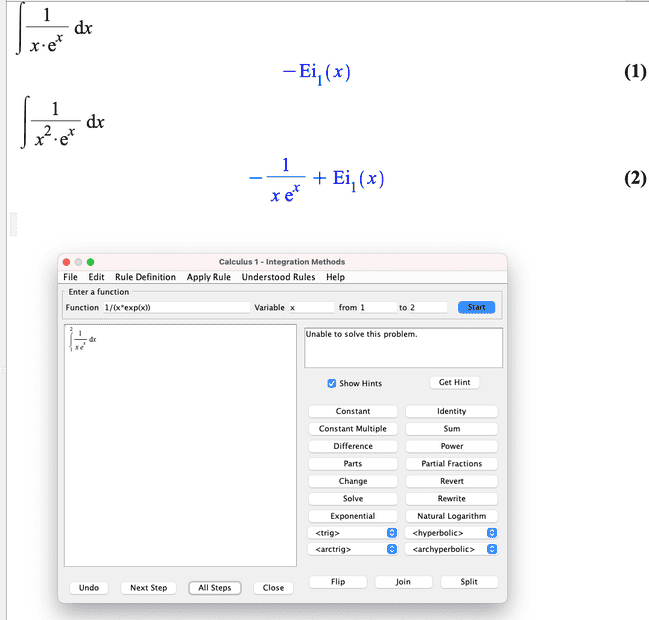
The window on the bottom is a sort of "math tutor" in Maple that shows all the steps in the calculation of the integral. However, for some integrals this step-by-step isn't available.
Now ##i_1(x)## is probably some variable defined within the depths of the dungeons of Maple documentation.
Still, what technique for solving integrals works for these integrals?
The general solution to the associated homogeneous equation is thus
$$y_h(x)=e^{-x}(c_1+c_2x)\tag{1}$$
Now we only need to find one particular solution of the non-homogeneous equation.
The righthand side of the non-homogeneous equation, call it ##R(x)##, is not a polynomial, nor does it fall in the category of ##p(x)e^{mx}## with ##p## being a polynomial. These are perhaps the two easiest special cases of ##R(x)## to solve because they can be solved by the method of undetermined coefficients.
##R(x)## is also not an exponential multiplied by an expression containing ##\sin## and/or ##\cos##, which can also be solved by the method of undetermined coefficients.
Thus, I have chosen to solve using a more general method based on the following theorem in Apostol's Calculus, Volume I
We have ##v_1(x)=1## and ##v_2(x)=x## as our solutions to ##L(y)=0##, ie the homogeneous equation.
The Wronskian of ##v_1## and ##v_2## is
$$W(x)=
\begin{vmatrix}
1 & 0\\
x & 1
\end{vmatrix}=1
\tag{2}$$
Thus,
$$t_1(x)=-\int x\cdot\frac{e^{-x}}{x^2}dx=\int\frac{e^{-x}}{x}dx\tag{3}$$
$$t_2(x)=\int \frac{e^{-x}}{x^2}dx\tag{4}$$
How do we solve these integrals?
Math software doesn't get me very far:
The window on the bottom is a sort of "math tutor" in Maple that shows all the steps in the calculation of the integral. However, for some integrals this step-by-step isn't available.
Now ##i_1(x)## is probably some variable defined within the depths of the dungeons of Maple documentation.
Still, what technique for solving integrals works for these integrals?