Solving for Tension & Angles in Ball Mass Problem: Help Needed!

Click For Summary
SUMMARY

The discussion focuses on calculating the tension and angles in a system involving two balls with different masses, specifically mass m and mass 2m. The relationship between the angles θ1 and θ2 is established through the equation m1*g*sinθ1 = m2*g*sinθ2, leading to sinθ1 = 2*sinθ2. Given the constraint that the sum of the angles θ1 and θ2 equals 2 radians, the problem can be solved by substituting θ2 with (2 - θ1) in the derived equation. This results in a definitive method to find the angles based on the mass ratio.

PREREQUISITES
  • Understanding of basic physics concepts, particularly forces and tension.
  • Familiarity with trigonometric functions and their applications in physics.
  • Knowledge of mass and gravitational force relationships.
  • Ability to solve equations involving multiple variables.
NEXT STEPS
  • Study the principles of tension in strings and ropes in physics.
  • Learn about the applications of trigonometry in solving physics problems.
  • Explore systems of equations and methods for solving them.
  • Investigate the dynamics of systems with multiple masses and their interactions.
USEFUL FOR

Students studying physics, particularly those focusing on mechanics, as well as educators and anyone interested in solving complex tension and angle problems in mass systems.

385sk117
Messages
50
Reaction score
0
http://ruliweb6.nate.com:8080/ruliboard/gup/img_link7/436/435945_1.jpg

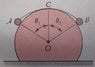
Ball A B
Mass m 2m

Length of tread is 2R where R is the radious of the Circle.
I have to find the tension on the tread and angles
I could have found the angles by assuming that the angle 1 and angle 2 are same
but as balls' masses are different, the angles must be different as well, and if they are different i don't think i can find the angle...
Any helps? Please TT
 

Attachments

  • 1.jpg
    1.jpg
    9.7 KB · Views: 455
Last edited by a moderator:
Physics news on Phys.org
Ball comes rest when
m1*g*sinθ1 = m2*g*sinθ2.
It is given that m2 = 2m1
So sinθ1 = 2*sinθ2...(1)
Length of the thread is 2R and radius is R.
So (θ1 + θ2) = 2R/R = 2 rad.
Put θ2 = (2 - θ1) in the eq.1 and solve for θ1.
 

Similar threads

Tension in a deformed cylindrical bag on a surface
  • · Replies 18 ·
Replies
18
Views
2K
Resolving forces: Mass on a string
  • · Replies 4 ·
Replies
4
Views
4K
Finding Charge & Tension of a Suspended Cork Ball
  • · Replies 3 ·
Replies
3
Views
4K
What is the formula for tension at various angles in a constrained mass system?
  • · Replies 5 ·
Replies
5
Views
2K
System of two pulleys and three masses
  • · Replies 22 ·
Replies
22
Views
6K
Tension of wire attached to 45-kg ball.
  • · Replies 2 ·
Replies
2
Views
8K
Problem involving space elevators
  • · Replies 19 ·
Replies
19
Views
2K
Hanging pith balls on a thread...charge, Fg, Fe and tension
  • · Replies 2 ·
Replies
2
Views
4K
Solving Tetherball Problem: Find Tension & Angle θ
  • · Replies 5 ·
Replies
5
Views
4K
Circular wire with ball and spring problem
  • · Replies 6 ·
Replies
6
Views
2K