calvinnn
- 9
- 0
There was a question on my math test today and i didnt even understand the problem. I want to see if anyone else knows how to do it. So here it goes:
"Use Calculus to prove which vertex angle an isoseles triange the greatest area"
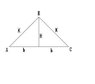
I think your supposed to find a equation for Area and Perimeter. Then take one of the equations and solve for a variable. Plug it into the next equation and then differentiate, like i would do on optimization problems, but i didnt know how to do it with this problem. Below is the figure given.
"Use Calculus to prove which vertex angle an isoseles triange the greatest area"
I think your supposed to find a equation for Area and Perimeter. Then take one of the equations and solve for a variable. Plug it into the next equation and then differentiate, like i would do on optimization problems, but i didnt know how to do it with this problem. Below is the figure given.