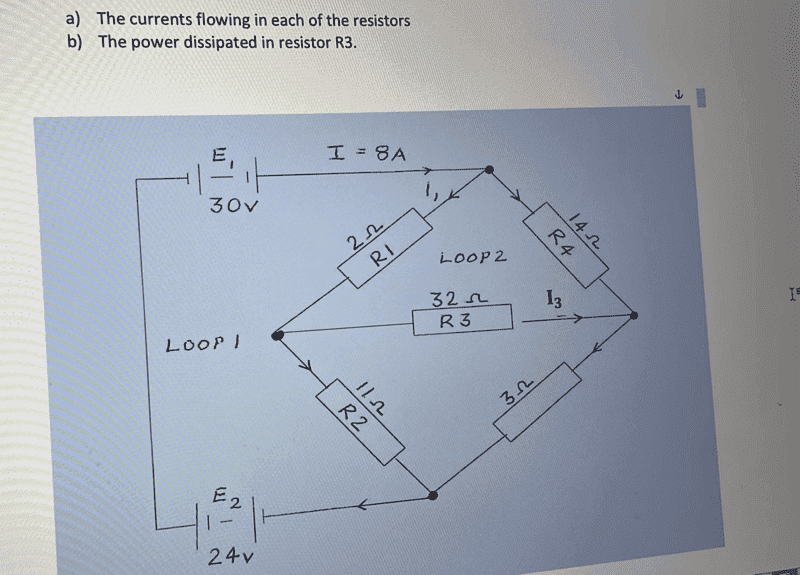
NikitaMazepin said:
I thought I2 + I3 - I4 = 0 by imagining the top part of the circuit on its own as a closed loop. This is probably wrong.
Kirchhoff's laws are broken down into two groups:
Kirchhoff's Current Law (KCL): The currents flowing into any circuit node sum to zero.
Kirchhoff's Voltage Law (KVL): The voltage drops around any circuit loop sum to zero.
So, don't mix up currents and loops or voltages and nodes, these won't give useful equations.
Then, at each circuit node you can generate an equation with KCL, like ## I_2 + I_5 = I_0 = 8 A ##. Since this network has 4 nodes* you'll get 4 equations this way. Notice that each term in these equations is a current. If I saw ## I_6 + I_8 +R7I_7 =0 ##, I would immediately know it was wrong because ## R7I_7 ## is a voltage and it doesn't make much sense to add a voltage to a current.
For each circuit loop you can generate an equation with KVL, like ## 2I_1 + 32I_3 - 14I_4 = 0 ##. Since this network has 3 (independent, unique) loops you'll get 3 more equations this way.
For simple components, like resistors, we often use the shorthand of naming the voltage across a resistor as the resistance times the current, like ## 14I_4 ##. But this is skipping the more rigorous approach of naming the voltage (potential) at each node. This would look like ## (V_A - V_B) + (V_B - V_C) +(V_C - V_D) = 0 ## (KVL) and ## (V_A -V_B) = I_{17}R17 ## (Ohm's Law), for example. People rarely do this verbose approach, but it's important to know the steps you may choose to skip. Likewise, there may be a very simple circuit node equation like ## I_3 + I_4 = I_5 ##, which will make some choose to just immediately substitute ## (I_3 + I_4) ## for the label ## I_5 ##. Again this is skipping steps, which is fine if you know that's what you're doing. However, if you get confused, go back and try it again with more basic steps.
So, having labeled all of the variables in your network, you can write down a bunch of equations in a rather mechanical process. Often the more you think about it the greater the chance that you will make a simple mistake, usually a sign error.
This process will actually generate more equations than you actually need. some are redundant and can be ignored.
* I've ignored the node that might (or might not) be between the batteries. Nodes with only two connections are usually ignored, since the equations that result are too simple to be very meaningful, like ## I_8 = I_9 ##. Also note that the voltage across all of the batteries is 54V, not the 30V you used initially.