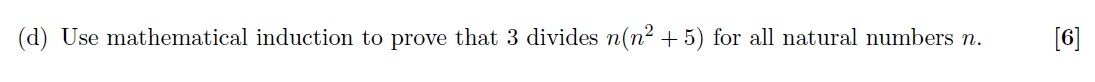SUMMARY
This discussion focuses on solving a mathematical induction problem involving the expression \( n(n^2 + 5) \) and proving its divisibility by 3. The participants outline the necessary steps for both the base case and the inductive step, emphasizing the importance of correctly stating the induction hypothesis. Key techniques include rewriting expressions for clarity and using \( f(n) = n(n^2 + 5) \) to facilitate the proof process. A link to a detailed outline of induction proof is also provided for further reference.
PREREQUISITES
- Understanding of mathematical induction principles
- Familiarity with algebraic manipulation of polynomials
- Ability to formulate and state induction hypotheses
- Knowledge of divisibility rules, specifically for the number 3
NEXT STEPS
- Study the principles of mathematical induction in detail
- Practice rewriting algebraic expressions for clarity in proofs
- Learn how to formulate induction hypotheses effectively
- Explore examples of mathematical induction proofs involving divisibility
USEFUL FOR
Students of mathematics, educators teaching proof techniques, and anyone seeking to improve their understanding of mathematical induction and its applications in problem-solving.