c.teixeira
- 39
- 0
I have been reading Ordinary Differential Equations (Pollard) from Dover.
The chapter I am in, is called Problems Leading to Differential Equations of The First Order - Geometric Problems.
Problem :
Find the family of curves with the property that the area of the region bounded by the x-axis , the tangent line drawn at a point P(x,y) of a curve of the family and the projection of the tangent line on the x-axis has a constante value A.
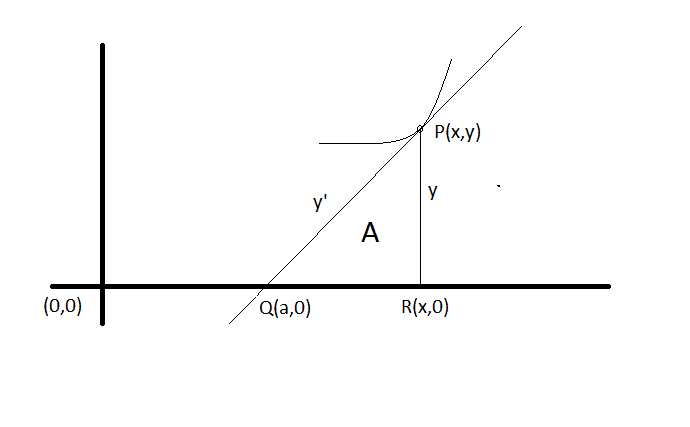
image hosting png
In the solution, they say the equation of the tangent line is y / (x - a) = y'
They then solve, for a:
a = x - (y/y')
Afterwards, they obtain the distance QR = y/y'
Therefore they have the area of the triangle. They integrate, bla blabla.
Now, when I first looked this, it seemed pretty simple and straighforward. I understood every step. It was an elementary problem.
But, today I gave it a second look, and now I just don't agree with the solution.
---------------
Well, my question is y = mx + b;
but m = y'.
so, y = y' x + b.
I don't agree with this since y defines the equation of the tangent line BUT y' defines the derivative of THE CURVE. therefore in my viewing, when they, in the solution, reach to QR = y/y', and then integrate they are mixing a fuction and a derivative of a diferent fuction.
So, where is my reasoning wrong?
Perhaps I should sleep more. ;D
Thanks for all the explanations!
The chapter I am in, is called Problems Leading to Differential Equations of The First Order - Geometric Problems.
Problem :
Find the family of curves with the property that the area of the region bounded by the x-axis , the tangent line drawn at a point P(x,y) of a curve of the family and the projection of the tangent line on the x-axis has a constante value A.
image hosting png
In the solution, they say the equation of the tangent line is y / (x - a) = y'
They then solve, for a:
a = x - (y/y')
Afterwards, they obtain the distance QR = y/y'
Therefore they have the area of the triangle. They integrate, bla blabla.
Now, when I first looked this, it seemed pretty simple and straighforward. I understood every step. It was an elementary problem.
But, today I gave it a second look, and now I just don't agree with the solution.
---------------
Well, my question is y = mx + b;
but m = y'.
so, y = y' x + b.
I don't agree with this since y defines the equation of the tangent line BUT y' defines the derivative of THE CURVE. therefore in my viewing, when they, in the solution, reach to QR = y/y', and then integrate they are mixing a fuction and a derivative of a diferent fuction.
So, where is my reasoning wrong?
Perhaps I should sleep more. ;D
Thanks for all the explanations!