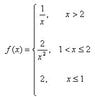Discussion Overview
The discussion revolves around determining the differentiability of a function at specific values of x. Participants explore the relationship between continuity and differentiability, and the necessary conditions for a function to be differentiable, including the evaluation of one-sided limits.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant suggests checking for continuity as a preliminary step in determining differentiability.
- Another participant claims there are issues with continuity at x=0, 1, and 2, but does not provide specific reasoning initially.
- A different participant argues that the function is continuous at x=1 and x=2, providing limits to support their claim.
- There is a suggestion to focus on points where the derivative may not exist rather than continuity alone.
- One participant emphasizes the importance of understanding the definition of differentiability and asserts that the function is continuous, challenging the claim of discontinuity.
- Another participant proposes checking the limits of the derivatives from both sides at x=1 and x=2 to assess differentiability.
Areas of Agreement / Disagreement
Participants express differing views on the continuity of the function at certain points, particularly at x=1, 2, and 0. The discussion remains unresolved regarding the specific values of x where the function is differentiable.
Contextual Notes
There are unresolved assumptions about the function's behavior at the specified points, and the discussion includes differing interpretations of continuity and differentiability.