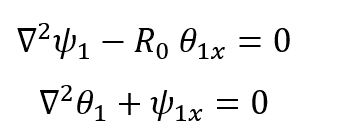Discussion Overview
The discussion revolves around solving a system of two partial differential equations (PDEs) related to hydrodynamic stability. Participants explore analytical methods for addressing these equations, including boundary conditions and the implications of stability definitions.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant requests help with solving a system of PDEs analytically, questioning if there is a general method for such problems.
- Clarifications are sought regarding notation, specifically whether certain symbols represent partial derivatives.
- Concerns are raised about the lack of information regarding boundary conditions, the domain, and functional spaces necessary for solving the PDEs.
- Another participant suggests that the problem involves normal modes and proposes a specific form for the solutions based on boundary conditions.
- There is a discussion about the definition of stability, with one participant expressing skepticism about the formulation of boundary conditions and the nature of the variables involved.
- A later reply discusses the potential connection of the PDEs to marginal stability in Rayleigh-Benard convection, suggesting a method to convert the PDEs into a system of ordinary differential equations (ODEs) for further analysis.
- Participants note the need for additional boundary conditions to properly analyze the system, highlighting the complexity of the problem.
Areas of Agreement / Disagreement
Participants express differing views on the formulation of boundary conditions and the interpretation of stability in the context of the problem. There is no consensus on the correct approach or the validity of the proposed methods.
Contextual Notes
Limitations include the absence of complete boundary conditions and the potential misinterpretation of variables. The discussion reflects uncertainty regarding the nature of the problem and the assumptions made by participants.