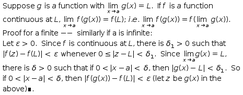Yankel
- 390
- 0
Hello
I need some help with this question, I don't know where to start...
The function f(x) is continuous over 0<=x<infinity and satisfy:
\[\lim_{x\to\infty }f(\frac{1}{ln(x)})=0\]
which conclusion is correct:
1. f(x)=1/ln x
2. f(x)=x
3. f(0)=0
4. f(infinity)=0
5. f(1) = infinity
thanks !
I need some help with this question, I don't know where to start...
The function f(x) is continuous over 0<=x<infinity and satisfy:
\[\lim_{x\to\infty }f(\frac{1}{ln(x)})=0\]
which conclusion is correct:
1. f(x)=1/ln x
2. f(x)=x
3. f(0)=0
4. f(infinity)=0
5. f(1) = infinity
thanks !