g9WfI
- 13
- 4
- Homework Statement
- A stone is thrown horizontally at 15 m/s from the top of a vertical cliff, 50 m above the sea. Calculate the distance from the bottom of the cliff to the place where the stone hits the water. g = 9.8 m/s^2
- Relevant Equations
- trig, suvat
Here is my attempt at the vector diagram:
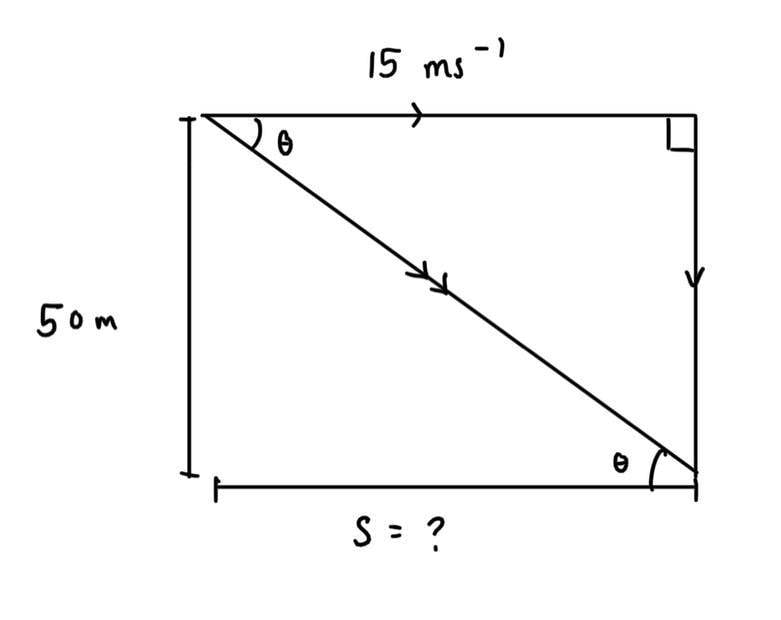
Could anyone give me any clues as to where to go from here? Is this diagram correct?
I tried finding θ using inverse tan 50/15 but I don't think I can do that because that's mixing up velocity and displacement.
EDIT: I copied and pasted the incorrect mark scheme here.
Correct mark scheme:
For the fall, s = 50 m, u = 0, v = ?, a = 9.8 m s–2 , t = ?
s = ut + ½at2 ⇒ 50 m = 0 + 4.9 m s-2 × t 2 ⇒ t 2 = 50 m ÷ 4.9 m s–2 = 10.2 s2
t = √(10.2 s2 ) = 3.19 s
horizontally, s = ut = 15 m s–1 × 3.19 s = 48 m (2 s.f.)
How do I find the corresponding displacements/velocities of the vectors with only this information?
I don't know if I'm making much sense, but I don't understand how to get the displacement from velocity;
I know s = vt but I'm not really getting anywhere with my working.
Could anyone give me any clues as to where to go from here? Is this diagram correct?
I tried finding θ using inverse tan 50/15 but I don't think I can do that because that's mixing up velocity and displacement.
EDIT: I copied and pasted the incorrect mark scheme here.
Correct mark scheme:
For the fall, s = 50 m, u = 0, v = ?, a = 9.8 m s–2 , t = ?
s = ut + ½at2 ⇒ 50 m = 0 + 4.9 m s-2 × t 2 ⇒ t 2 = 50 m ÷ 4.9 m s–2 = 10.2 s2
t = √(10.2 s2 ) = 3.19 s
horizontally, s = ut = 15 m s–1 × 3.19 s = 48 m (2 s.f.)
How do I find the corresponding displacements/velocities of the vectors with only this information?
I don't know if I'm making much sense, but I don't understand how to get the displacement from velocity;
I know s = vt but I'm not really getting anywhere with my working.
Last edited: