Some questions regarding the ADI Method

[Telemachus]

Hi there. I am writing a code to solve the diffusion equation in two dimensions using the Alternate Directions Implicit method: https://en.wikipedia.org/wiki/Alternating_direction_implicit_method

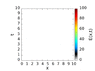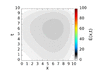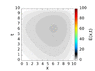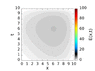
I haven't finished to write the code yet, but I am trying to be the most general as possible. However, in the bibliography I have found almost exclusively the case for homogeneous media, and the stability analysis is done for that case, in which the matrices to be inverted are symmetric. I know that going to 3D is complicated because the Peaceman-Rachford scheme isn't stable. However, I wanted to know if there is any analysis reported in the bibliography for the inhomogeneous media case. I will finish to write the code and experiment with it by my self, but I was trying to avoid the analytical part. I have already written the algorithm, so I'm just coding right now.

I also would like to pose the question on why the homogeneous case is so widely reported, when the inhomogeneous is much more general and useful I think. Is there any numerical trick to use the homogeneous media solution to solve the inomogeneous media case in an efficient way? perhaps recursively, using finite differences?

Thanks in advance.

 

[Telemachus]

Well, I have written the code and it is clearly stable. It converges to the analytic solution. I have manufactured a solution with inhomogeneous diffusion and absorption coefficients, so I have corroborated by numerical experimentation that it is stable. But if there is any reported analytic proof it would be nice.

So, here are the plots (its x,y, not x,t). The error can be reduced by writing well the boundary conditions, in the way I have written it it's only first order in $dt$, written in other way can be done $dt^2$.

Numerical:

Analytic:

Error: