Spectrum classification and dimension reduction

[roam]

I am trying to distinguish two different plant species based on their chemical signature using statistical signal classification. This is what the average curves of two species look like with their standard deviation bounds:

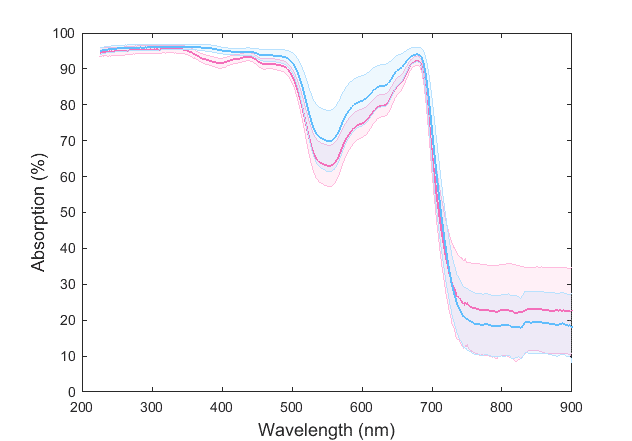
These spectra are made up of ~1400 points. So it was suggested to me to use a dimension reduction technique, instead of using a ~1400-dimensional vector space.

So, what are the problem that could occur if the multidimensional data space is large?

Also, if we were to classify based on only a few points (and throw away the rest) — would that not increase the likelihood of misclassification errors? Because we have fewer features to consider. I presume dimension reduction works differently because we are not throwing away any data.

Any explanation is greatly appreciated.

 

[MarneMath]

Broadly speaking high dimensional data can be problematic for two main reasons. First, the computational cost to learn and inference may be high and secondly it can lead to over-fitting. Dimensional reduction attempts to resolve these two issues while still preserving most of the relevant information (--based on assumptions in the technique).

There's a few ways you can get a reduced space. You can apply feature selection as you would in a linear regression type model. There you can use your common forward/backward selection process or some variant of chi-squared score or whatever metric you want to use for importance and use the to determine the top K features. You can also do a more matrix factorization technique like Trunciated SVD or PCA (of which SVD is a generalization) to common features into lower lower dimensions. This is commonly done in text processing as a way to mitigate similar words (ie bird vs birds). There's also feature projection, where you can use random projects or tree embeddings to project your higher features into a lower dimensional representation.

Whatever you choose to do (based on the data you have), the key idea is the same. You're trying to eliminate features that may have been encoded in other features implicitily or explicitly and return a space that is more general that may lead to be generalization on a validation and test set. Each technique uses different assumptions and it's up to you to decide what works best for your goals and data.

In my personal work life, I commonly take 100k-200k feature matrix down to 400 features. While accuracy metrics may drop on my training set, there tends to be a notable ability to perform consistently well on unseen data, which is reality is what you really care about.

 

[roam]

Thank you for your explanations.

Could you explain what you mean by saying that it could lead to over-fitting?

Also, when we are dealing with spectra (as in my problem), what sort of features could get eliminated?

I believe the regions where there is a complete overlap between the two clusters are useless for classification. For instance, in my graph, this would be the 750–900 nm range (the NIR plateau). Would techniques such as PCA automatically exclude these regions?

In these overlapping intervals, we cannot use the Euclidean distance between the two pattern sets to classify signals (this is apparently the simplest and most intuitive way to classify).