Spherical capacitor with dielectrics

[Karl86]

Homework Statement

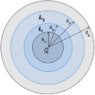
Consider the following system:

which consists of a conducting sphere with free charge , a dielectric shell with permittivity $\epsilon_1$, another dielectric shell with permittivity $\epsilon_2$ and finally a conducting spherical shell with no free charge.

Homework Equations

$D = \epsilon_0 E+P$
$\sigma_b=P \cdot \hat{n}$

The Attempt at a Solution

After finding $D=\frac{Q}{4\pi r^2}\hat{r}$, I calculated the polarization vector $P_1,P_2$ on each region to be
$$P_1=\left(1-\frac{\epsilon_0}{\epsilon_1}\right)\frac{Q}{4\pi r^2}\hat{r} \\
P_2=\left(1-\frac{\epsilon_0}{\epsilon_2}\right)\frac{Q}{4\pi r^2}\hat{r} $$
and the surface charge due to bound charges to be
$$ \sigma_{b_1}=\begin{cases}\frac{\epsilon_0 \chi_1 Q}{4\pi \epsilon_1 R_2^2} & \text{on outer surface} \\ -\frac{\epsilon_0 \chi_1 Q}{4\pi \epsilon_1 R_1^2} & \text{on inner surface} \end{cases}$$
$$ \sigma_{b_2}=\begin{cases}\frac{\epsilon_0 \chi_2 Q}{4\pi \epsilon_2 R_3^2}\hat{r} & \text{on outer surface} \\
-\frac{\epsilon_0 \chi_2 Q}{4\pi \epsilon_2 R_2^2}\hat{r} & \text{on inner surface} \end{cases}$$
$\rho_b=0$ for both dielectrics because the divergence of $P_i$ is zero. Now I want to see that the overall induced charge is zero. I try to do this by integrating the surface distributions on each sphere and I get that the total charge induced by the dielectric 1 is $\frac{\epsilon_0 \chi_1 Q}{\epsilon_1}$ at $R_2$, $-\frac{\epsilon_0 \chi_1 Q}{\epsilon_1}$ at $R_1$ and for the dielectric 2 it's $\frac{\epsilon_0 \chi_2 Q}{\epsilon_2}$ at $R_3$, $-\frac{\epsilon_0 \chi_2 Q}{\epsilon_2}$ at $R_2$. This seems to add up to zero, but I wonder whether these are the only induced charges in this setup or I'm forgetting something. Also: is integrating like that just the right way to compute the induced charge?
Thanks if you'll find time to help me somehow.

 

[kuruman]

This seems to add up to zero, but I wonder whether these are the only induced charges in this setup or I'm forgetting something.

See if there are induced free charges on the surfaces of the outer conducting shell at $r=R_3$ and $r=R_4$. Use the boundary condition on the normal component of $\vec D$ to find what they are.

Also: is integrating like that just the right way to compute the induced charge?

Yes except surface charge density is a scalar quantity. You have a unit vector $\hat r$ attached to $\sigma_{b_2}$ which does not belong. I'm sure it's a typo.

 

[Karl86]

See if there are induced free charges on the surfaces of the outer conducting shell at $r=R_3$ and $r=R_4$. Use the boundary condition on the normal component of $\vec D$ to find what they are.

Yes except surface charge density is a scalar quantity. You have a unit vector $\hat r$ attached to $\sigma_{b_2}$ which does not belong. I'm sure it's a typo.

Thanks a lot for your reply. For sure that's scalar and that was a typo. About your first remark: I was inclined to think that the total induced charge at $R_3$ would be equal in value to the one induced by the dielectric at $R_3$ and of opposite sign, because there is indeed some free charge due to the fact that the last spherical shell is a conductor. Similarly at $R_4$. Is this wrong?

 

[kuruman]

Thanks a lot for your reply. For sure that's scalar and that was a typo. About your first remark: I was inclined to think that the total induced charge at $R_3$ would be equal in value to the one induced by the dielectric at $R_3$ and of opposite sign, because there is indeed some free charge due to the fact that the last spherical shell is a conductor. Similarly at $R_4$. Is this wrong?

It is correct. You might wish to calculate the free charge distributions and see what they are. Do you know how to do that?

 

[Karl86]

It is correct. You might wish to calculate the free charge distributions and see what they are. Do you know how to do that?

Hmm. I don't really know how to calculate them. I thought it was just a consequence of saying that it had to be the opposite of the total charge induced by the dielectric and that would be it.

 

[kuruman]

The free surface charge density at the boundary between regions 1 and 2 is given by $\sigma=(\vec D_2-\vec D_1)\cdot \hat n$ where $\hat n$ is the normal to the boundary and is directed from 1 into 2. See https://en.wikipedia.org/wiki/Interface_conditions_for_electromagnetic_fields

 

[Karl86]

The free surface charge density at the boundary between regions 1 and 2 is given by $\sigma=(\vec D_2-\vec D_1)\cdot \hat n$ where $\hat n$ is the normal to the boundary and is directed from 1 into 2. See https://en.wikipedia.org/wiki/Interface_conditions_for_electromagnetic_fields

In my case $D=\frac{Q}{4\pi r^2}\hat{r}$ in 2 and $0$ in 1 and $\hat{r} \cdot \hat{n} = 1$ so $(\vec D_2-\vec D_1)\cdot \hat n = \frac{Q}{2\pi R_1^2}$, right? Is it correct to pick the value of $D$ right inside the boundary between the regions?

 

[kuruman]

In my case $D=\frac{Q}{4\pi r^2}\hat{r}$ in 2 and $0$ in 1 and $\hat{r} \cdot \hat{n} = 1$ so $(\vec D_2-\vec D_1)\cdot \hat n = \frac{Q}{2\pi R_1^2}$, right? Is it correct to pick the value of $D$ right inside the boundary between the regions?

It is correct to do that, but there is another typo, the $2$ in the denominator should be a $4$. What is the total charge on the surface at $R_1$? Repeat for the interfaces at $R_3$ and $R_4$.

 

[Karl86]

It is correct to do that, but there is another typo, the $2$ in the denominator should be a $4$. What is the total charge on the surface at $R_1$? Repeat for the interfaces at $R_3$ and $R_4$.

$Q$, $-Q$,$Q$. Ok, I think I got the gist of it, at least it feels much clearer now thanks to you. One quick question that I think is not worth opening a thread about. Is the normal component of $P$ discontinuous at the interface of the two dielectrics?

 

[kuruman]

$Q$, $-Q$,$Q$. Ok, I think I got the gist of it, at least it feels much clearer now thanks to you. One quick question that I think is not worth opening a thread about. Is the normal component of $P$ discontinuous at the interface of the two dielectrics?

You can answer that by yourself. Look at your expressions for $\vec P_1$ and $\vec P_2$ in post #1. Evaluate each expression separately at $r=R_2$. If the two expressions are not equal then the normal component of $P$ is discontinuous; if they are equal then it is continuous.

 

[Karl86]

You can answer that by yourself. Look at your expressions for $\vec P_1$ and $\vec P_2$ in post #1. Evaluate each expression separately at $r=R_2$. If the two expressions are not equal then the normal component of $P$ is discontinuous; if they are equal then it is continuous.

Yeah, I was confused because it seemed impossible for $P$ to be discontinuous but not $D$, but now I realized that the normal component of $E$ is discontinuous too, so that fixes things. Thanks