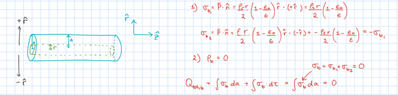Calculating Bound Charge Density & Polarization

[Gustav]

Homework Statement

A long straight non-conductive cylindrical rod with radius a has the permittivity ε. It is given by a uniform free space charge density ρ_f. (That this charge density is "free" means that it did not arise through polarization. However, the charges that build up ρ_f are not moving freely, but ρ_f has the same constant value throughout the rod.) Determine all bound charge densities by using the cylinder symmetry and verify from these that the total bound charge per unit length of the

Relevant Equations

\sigma_b = P * n
\rho_b = \nabla * P

I have already calculated the polarisation that is
$$ \mathbf{P} = \frac{\rho_f r}{2} \left( 1 - \frac{\epsilon_0}{\epsilon} \right) \hat{r} . $$
I tried to use the following formulas to calculate the density bound charges. For the surface bound charge I got:
$$ \sigma_{b1} = \mathbf{P} \cdot \hat{n} = + \frac{\rho_f r}{2}\left( 1 - \frac{\epsilon_0}{\epsilon} \right), \ \ \ \ \sigma_{b2} = - \frac{\rho_f r}{2}\left( 1 - \frac{\epsilon_0}{\epsilon} \right). $$
As for the volume bound charge, I assumed that we have a uniformal polarisation since the free charge is constant everywhere in the material, which will give us a volume bound charge equal to zero,
$$ \rho_b = \nabla \cdot \mathbf{P} = 0. $$
Also for calculating the total bound charge I got something like this:
$$ Q_{tot, b} = \int \sigma_b da + \int \rho_b d\tau = \int \sigma_b da = \int (\sigma_{b1} + \sigma_{b2}) da = 0 $$
But I feel like I have misunderstood the question, and feel unsure about my answer, is there anything wrong with it? Also I am attaching a file bellow of the solution.

 

[member 553083]

Can someone please explain how they got the answer?A:The surface bound charge is easy. The surface of the sphere is the same in both cases, so it doesn't matter if you have an external field or not. The surface charge is:$$\sigma_b = \sigma_{b1} + \sigma_{b2} = \mathbf{P}\cdot \mathbf{\hat n} = \frac{\rho_f r}{2}\left( 1 - \frac{\epsilon_0}{\epsilon} \right) + \frac{\rho_f r}{2}\left( 1 - \frac{\epsilon_0}{\epsilon} \right) = \rho_f r \left( 1 - \frac{\epsilon_0}{\epsilon} \right)$$Now for the volume bound charge, we need to calculate $\nabla \cdot \mathbf{P}$. Since the polarization is uniform, then the divergence is zero: $$\nabla \cdot \mathbf{P} = 0$$Therefore, the volume bound charge is zero. Finally, the total bound charge is just the surface bound charge multiplied by the area of the sphere: $$Q_{tot,b} = \sigma_b A = \rho_f r \left( 1 - \frac{\epsilon_0}{\epsilon} \right) 4 \pi r^2 = 4 \pi \rho_f r^3 \left( 1 - \frac{\epsilon_0}{\epsilon} \right) $$