Spherical Coordinates: Understanding Theta Equation

[MattRob]

So, I was curious about this and found more or less what I was looking for here: http://electron9.phys.utk.edu/vectors/3dcoordinates.htm

Except, something is bothering me about those equations. At the very bottom, the equation for Theta in a spherical coordinate system; shouldn't it be
\theta = {tan^{-1}}( \frac{\sqrt{{x^{2}}+{y^{2}}}}{z})
instead of
\theta = {tan^{-1}}( \frac{z}{\sqrt{{x^{2}}+{y^{2}}}})

(The image in question)

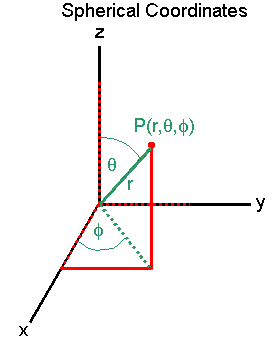
Because {tan^{-1}}( \frac{opposite}{adjacent}) = \theta , and looking at angle \theta , the line opposite of it is exactly equal to \sqrt{{x^{2}}+{y^{2}}} , and the line adjacent to it equal to z.

So I'm wondering if I'm in error (and how so if I am) or if the linked page is.

 

[jtbell]

You are correct. That equation on that page is in error.

 

[Astrum]

It appears that page is wrong. You're right, the correct relation is

$\theta = \tan ^{-1}\left( \frac{\sqrt{x^2 +y^2 }}{z}\right)$.

You could also write it as $\theta = \cos ^{-1} \left(\frac{z}{\sqrt{x^2 +y^2 +z^2 }}\right)$Edit: Darn you, jtBell, you beat me by seconds!

 

[Simon Bridge]

yep... it sure looks like they've got their sides mixed up.
However, it is more usual to use $\theta = \cos^{-1}(z/r):r=\sqrt{x^2+y^2+z^2}$

 

[MattRob]

Thanks very much for all the replies! Are the equations for the x, y, and z components from a spherical coordinate system correct on that page, though?

And why is the $\theta = \cos ^{-1} \left(\frac{z}{\sqrt{x^2 +y^2 +z^2 }}\right)$ approach more common? The \theta = {tan^{-1}}( \frac{\sqrt{{x^{2}}+{y^{2}}}}{z}) one has less terms. Something to do with higher mathematics?