Spontaneous Symmetry Breaking and quantum mechanics

[arivero]

TL;DR

links and general commentary

Confronted with my inability to grasp Witten's Susy QM examples of supersymmetry breaking, I concluded that the problem was that I was not understanding spontaneous symmetry breaking in simpler contexts.
It seems that SSB is not possible in QM because of tunneling between the different states, and that it becomes possible in QFT because the transition probability becomes zero in infinite volume, albeit almost no textbook takes the time to prove it, just state it -or not-.
The best question I have found is this one in PhysicsExchange, and it links to an interesting paper couple of papers by Landsman

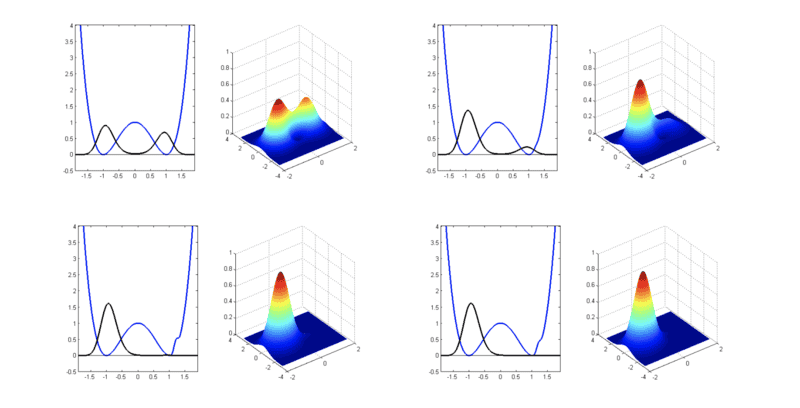
calculating the flea, they say in the cat instead of the elephant It also links to a preprint by Thirring and Narnhofer, that mentions the case of SUSY QM.

The double (and multiple) well symmetry breaking in QM was taken with great interest in the eighties, I guess the sparks were Witten's Susy QM, Coleman instantons, and the analysis of Jona-Lasinio, Martinelli and Scoppola, as well as Barry Simon's "flea in the elephant" for analysts. It was revisited periodically each time a generation finished their formative years. I see a revisit by M-K in 1992, by myself in 1994 (uploaded later), Casahorran in 2001 (triple well) or Alhendi-Lashin in 2004. Related topics as transparent or shape invariant potentials and delta potentials are also revisited frequently. Still I do not find a consistently complete approach to the topic, including things as Witten's spontaneous susy breaking, where the partner has been fully collapsed out and is not a normalised state anymore, or the impossibility of an analogous of Goldstone theorem for localization.

 

[DrDu]

The simple picture is that in QFT you are dealing with infinite coupled copies of the QM double well problem, quasi an Ising problem. Hence if the overlap of the two wavefunctions in the two wells is x<1, in QFT the overlapp in QFT is $\lim_{n \to \infty} x^n =0$. Hence there are two ground states which have no overlap and no operator which can only change the occupancy of a finite number of double wells, can have matrix elements between these two states. So the two ground states live in different Hilbertspaces.
Personally, I like the carefull anaysis by Strocchi: https://link.springer.com/book/10.1007/978-3-540-73593-9

 

[malawi_glenn]

QFT because the transition probability becomes zero in infinite volume

Source?

 

[arivero]

Source?

Good point, perhaps we could try to do a collaborative table telling the claims contained in each textbook. I will keep editing the table if new textbooks are commented in the thread.

Book	Section	excerpt or comments
Huang, "Quarks Leptons & Gauge Fields", 2nd edition	3.2 Spontaneous Breaking of Global Gauge Invariance	page 53: "The transition amplitude between vacua with different values of [latex]\alpha_0[/latex] vanishes for infinite spatial volume."
Peskin Schroeder, "An Introduction to Quantum Field Theory"	11.1 Spontaneous Symmetry Breaking.	No discussion
	11.3 to 11.5: the effective potential	pg 308 and figure 11.6 refer to metastable vacuum states, but only after the Effective Potential has been built. Volume is mentioned in eq. 11.50.
S. Weinberg, Quantum theory of Fields,	vol. 2, Chpt. 19	Note that only global symmetries can be spontaneously broken, not local gauge symmetries, although even Weinberg talks about spontaneous breaking of local gauge symmetries. (@vanhees71 )

 

[malawi_glenn]

Then why are checking for global minimum a thing in BSM Higgs physics modelleing? I.e. one puts theoretical restrictions on the parameter space of the model such that the potential does not have additional minima

 

[arivero]

Then why are checking for global minimum a thing in BSM Higgs physics modelleing? I.e. one puts theoretical restrictions on the parameter space of the model such that the potential does not have additional minima

Not sure, Huang also puts an example of a negative quartic, that should be a metastable state in x=0 in quantum mechanics and says that "would be true in particle quantum mechanics, but not in quantum field theory" because in this case "the decay rate of such an initial state in infinite space is infinite" and thus the metastable case does not even exist. It would seem that authors have considered that decays rates of metastable vacuum states are an advanced topic and excused discusion in textbooks.

To put more wood in the fire, some other textbools like to use the connection between vacua as a way to "proof" Goldstone theorem. So Donoghue-Golowich-Holstein pg 21: "Thus in the limit of infinite wavelength the excitation energy vanishes, yielding a Goldstone boson"

 

[malawi_glenn]

I can ask a former collegue who is working on similar research problems

 

[arivero]

I can ask a former collegue who is working on similar research problems

It is a bit of a labyrinth. Literally: Peskin-Schroeder say that other exotic effects come from "the topology" of the space of vacua. Once you leave the mexican hat, everything can happen, it seems.

 

[vanhees71]

I think the clearest discussion of spontaneous symmetry breaking is in

S. Weinberg, Quantum theory of Fields, vol. 2, Chpt. 19

Note that only global symmetries can be spontaneously broken, not local gauge symmetries, although even Weinberg talks about spontaneous breaking of local gauge symmetries. It's an unfortunate inaccuracy of language. One should rather talk about a "Higgsed local gauge symmetry" or "hidden local gauge symmetry", but that's another topic.

 

[DrDu]

Weinbergs Discussion is certainly correct. But him stressing the importance of degenerate vacua is misleading as in QFT vacua are generally highly degenerate.
In the Weinberg chair example, e.g., vaporization of the chair would lead to a gas with some given density. If we could switch off the interactions between the gas particles, this gas would form a vacuum state with unbroken rotational symmetry. However, in the thermodynamic limit, total angular momentum is not an observable, only angular momentum density is. We could change the angular momentum of an arbitrary (finite) number of gas particles without changing the state. Hence the ground state is degenerate even if symmetry is unbroken, but the structure of the ground states is different.
For the example of superconductivity this has been worked out very lucidly by Rudolf Haag, which is my favourite reference on the topic of broken symmetry:

Haag, R. (1962). The mathematical structure of the Bardeen-Cooper-Schrieffer model. Il Nuovo Cimento (1955-1965), 25(2), 287-299.

 

[vanhees71]

Another very pedagogical paper using the BCS model to discuss the important difference between spontaneous symmetry breaking and hidden local gauge symmetries is

https://arxiv.org/abs/cond-mat/0503400

 

[DrDu]

When Hendrik mentioned this paper before, I tended to start arguing, especially about section II. The rest of the paper is excellent. But maybe I finally see what I got wrong. I'll start a new thread to discuss this.

 

[A. Neumaier]

It seems that SSB is not possible in QM

There is a lot of SUSY for ordinary QM, and in all interesting cases, the SUSY is broken. See, e.g.,

• Cooper, F., Khare, A., & Sukhatme, U. (1995). Supersymmetry and quantum mechanics. Physics Reports, 251(5-6), 267-385. https://arxiv.org/pdf/hep-th/9405029.pdf

 

[arivero]

There is a lot of SUSY for ordinary QM, and in all interesting cases, the SUSY is broken. See, e.g.,

• Cooper, F., Khare, A., & Sukhatme, U. (1995). Supersymmetry and quantum mechanics. Physics Reports, 251(5-6), 267-385. https://arxiv.org/pdf/hep-th/9405029.pdf

Ah thanks for the reminiscence, I did some calculations for https://inspirehep.net/literature/355497 a preprint then. I guess I should check it again. It was a line of research starting from https://inspirehep.net/literature/18852 in the time that Boya was going back and forward to utexas, but I was never sure if it was susy for real or just factorisation method.

 

[A. Neumaier]

Ah thanks for the reminiscence, I did some calculations for https://inspirehep.net/literature/355497 a preprint then. I guess I should check it again. It was a line of research starting from https://inspirehep.net/literature/18852 in the time that Boya was going back and forward to utexas, but I was never sure if it was susy for real or just factorisation method.

The factorization method for exactly solvable QM systems can be interpreted in N=1 SUSY terms. This shows that SUSY is nothing spectacularly new.

 

[arivero]

Boya was particularly intrigued by the case where the superpotential is the sign function, so the two pairs are delta potential and delta barrier. I was assigned to look into it but I was never explicitly told to focus in susy pairings so I let it to pass. Surely it is done elsewhere in the literature multiple times; I find this kind of things resurface with a ten years periodicity.