Stability, phase portrait, bifurcations

  • Context: MHB 
  • Thread starter Thread starter ZiniaDuttaGupta
  • Start date Start date
  • Tags Tags
    Phase Stability
Click For Summary
SUMMARY

The discussion focuses on analyzing a one-dimensional ordinary differential equation (ODE) represented as X’ = f(x). Key tasks include identifying fixed points and their stability, drawing the phase portrait, and studying bifurcations of the modified ODE X’ = f(x) + α, where α is a real parameter. Participants are encouraged to determine bifurcation values of α and describe behavioral changes associated with these bifurcations. The discussion emphasizes the importance of visualizing the solutions and phase portraits for a comprehensive understanding.

PREREQUISITES
  • Understanding of ordinary differential equations (ODEs)
  • Knowledge of stability analysis in dynamical systems
  • Familiarity with phase portraits and their significance
  • Concept of bifurcations in mathematical modeling
NEXT STEPS
  • Study fixed point analysis in dynamical systems
  • Learn how to construct phase portraits for ODEs
  • Research bifurcation theory and its applications
  • Explore numerical methods for solving ODEs and visualizing solutions
USEFUL FOR

Students and researchers in mathematics, particularly those studying dynamical systems, as well as educators looking for examples of ODE analysis and bifurcation behavior.

ZiniaDuttaGupta
Messages
3
Reaction score
0
I am stuck with another one --

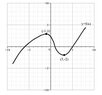
Assume that f(x) has the following graph: (for graph please see the attachment)
Consider the (1-dimensional) ODE:

X’ = f(x):

(a) Find all the xed points, and study their stability.

(b) Draw the phase portrait of the system, as well as the graphs of the solutions in all relevant cases.

(c) Study the bifurcations of the ODE

X’ = f(x) + α ; α € R - a parameter.

In particular, determine all the bifurcation values of α , and describe the change in behaviour before during and after each bifurcation. Make sure to draw the appropriate graphs
 

Attachments

  • Graph.jpg
    Graph.jpg
    10 KB · Views: 129
Physics news on Phys.org
I have reason to believe this is part of a graded assignment. Please contact me with your professor's contact information so that I can verify that it is okay for you to receive outside help with this question.

Best Regards,

Mark.
 

Similar threads

MHB What are the fixed points and stability of a non-linear system of ODEs?
  • · Replies 1 ·
Replies
1
Views
2K
How to draw phase portrait for 2x2 nonlinear system of DE?
  • · Replies 1 ·
Replies
1
Views
2K
MHB Differential equations stability
  • · Replies 2 ·
Replies
2
Views
2K
MHB Solve Linear System of ODEs | x(0)=x0,y(0)=y0,z(0)=z0
  • · Replies 1 ·
Replies
1
Views
2K
Want a book/notes that cover this syllabus (dynamical systems).
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Qualitative implications of parameter shift in non-autonomous ODE
  • · Replies 1 ·
Replies
1
Views
2K
Graduate Need help drawing phase portraits for coupled systems of ODEs
  • · Replies 2 ·
Replies
2
Views
12K
Constructing lagrangian and phase portrait
  • · Replies 1 ·
Replies
1
Views
2K
MHB Damped spring differental equation
  • · Replies 19 ·
Replies
19
Views
4K
Determine the stability of a fixed point of oscillations
  • · Replies 2 ·
Replies
2
Views
3K