Standard basis and other bases...

[fog37]

Hello,
I am review some key linear algebra concepts. Let's keep the discussing to 2D.
Vectors in the 2D space can be simplistically visualized as arrows with a certain length and direction. Let's draw a single red arrow on the page representing vector $X$, an entity that is independent of the basis choice:

We then can choose ANY pair of not collinear vectors to form a basis. Basis 1 has two basis vectors with coordinates $a=(1,0)$ and $b=(0,1)$. The basis vectors $a$ and $b$ have coordinates....Their coordinates are exactly $(1,0)$ and $(0,1)$ ONLY under the implicit assumptions that the two vectors are the basis vectors or a specific basis, basis 1 in this case.
If we consider the different basis 2, the basis vector $c$ and $d$ will also have coordinates $c=(1,0)$ and $d=(0,1)$ as long as we are under the assumption that the are themselves the basis vectors of a specific basis.

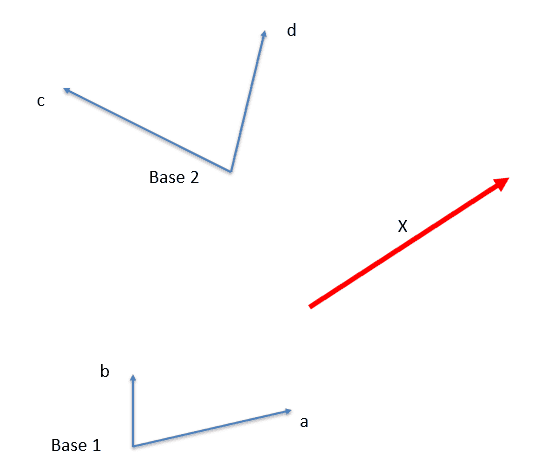
So the coordinates of a vector are always relative (to the basis we choose): if we arbitrarily decide that the basis we want to use is basis 1, then vectors $a$ and $b$ will be the basis vectors themselves with coordinates $(1,0)$ and $(0,1)$ and vectors $c$and $d$ will have different coordinates...Basis vectors always have coordinates $(1,0)$ and $(0,1)$ in their OWN basis and different coordinates in a different basis... This may seem obvious but I needed to flush it out to make sure I am indeed thinking correctly about it.

Orthogonal bases give concise representations of vectors in the vector space: every basis vector encodes a specific and independent piece of information about the vector. Some orthogonal bases provide more sparse representations that others...

Non-orthogonal bases can also be useful. To find the coefficients associated to a certain basis vector we need the vector itself, the basis vector, but also the other basis vectors....I am confused about that. In the case of orthogonal bases, we simply perform the dot product between the vector and the specific basis vector without involving other basis vectors....Involving them in what sense?

Thank YOU!

 

[hutchphd]

You have not defined an "orthogonal basis". Perhaps a less "wordy" explanation is useful. You need to define inner products and other stuff. What is the ultimate purpose of your review? What does review "concepts" mean? What level are you shooting for?

 

[WWGD]

I suggest fleshing it out :).
But, yes, the basis $\{(0,1),(1,0)\}$ does have the unique property that a vector $(a,b)$ will be represented , precisely, as $(a,b)$.
Is that what you were asking?

 

[BvU]

I seem to remember that two vectors can (and do) form a basis if the decomposition in components of  any vector is unique. Needs things like inner product and null vector to be defined.
Orthogonality and orthonormality are subsequent embellishments.

 

[fog37]

I suggest fleshing it out :).
But, yes, the basis $\{(0,1),(1,0)\}$ does have the unique property that a vector $(a,b)$ will be represented , precisely, as $(a,b)$.
Is that what you were asking?

This may be obvious, but the basis vectors belonging to a particular basis always coordinates $\{(0,1),(1,0)\}$. Basis vectors forming a different basis also have coordinates $\{(0,1),(1,0)\}$.

 

[hutchphd]

This gets back to the generaldefinition of a vector space over a field.
The choice of the standard basis is one of book-keeping mostly as I recall. You have settled on the particular vector space ${\mathbb R}^2$

 

[mathwonk]

notice that neither set of coordinates in either of your bases can tell you where your red arrow begins or ends. the difficulty is that you have defined a vector slightly incorrectly; i.e. a vector is not an arrow, but an equivalence class of arrows, all having then same length and direction, but beginning at any arbitrary point of the plane. thus an arrow is not a vector, but it does determine a vector, and perhaps this is what you meant.

 

[nuuskur]

every basis vector encodes a specific and independent piece of information about the vector

This is true for any basis not just an orthogonal one. Any vector has unique coordinates with respect to a given basis.

Some orthogonal bases provide more sparse representations that others

What does this mean?

In the case of orthogonal bases, we simply perform the dot product between the vector and the specific basis vector without involving other basis vectors....Involving them in what sense?

If $\{e_i\}$ is an orthonormal basis, then
$$x = \sum \langle x,e_i\rangle e_i$$
You do "involve other basis vectors".

 

[fog37]

This is true for any basis not just an orthogonal one. Any vector has unique coordinates with respect to a given basis.

What does this mean?


If $\{e_i\}$ is an orthonormal basis, then
$$x = \sum \langle x,e_i\rangle e_i$$
You do "involve other basis vectors".

Yes, I was referring to the fact that, in the case of an orthogonal basis, the coefficient for a specific basis vectors is calculated using the vector $x$ and the only the basis vector itself....

In the case of a non-orthogonal basis, I think the coefficient for a specific basis vector requires knowledge of the other basis vectors...

 

[Office_Shredder]

Yes, I was referring to the fact that, in the case of an orthogonal basis, the coefficient for a specific basis vectors is calculated using the vector $x$ and the only the basis vector itself....

In the case of a non-orthogonal basis, I think the coefficient for a specific basis vector requires knowledge of the other basis vectors...

Yes, it is true if I tell you v is part of an orthogonal basis with inner product <,> and ask what the coefficient of v is when representing u, you can figure it out without knowing what the rest of the basis is, and this is not true if the basis is not orthogonal in general.