Standard Model decompositions of larger group representations?

Click For Summary

Discussion Overview

The discussion revolves around the decomposition of larger group representations, specifically within the context of Grand Unified Theories (GUTs) and the Standard Model (SM) of particle physics. Participants explore how representations of gauge groups, such as SU(5), can be broken down into Standard Model gauge quantum numbers, and seek clarification on the methodologies and motivations behind these decompositions.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant notes the existence of Standard Model decompositions for SU(5) representations but expresses confusion about how these decompositions are determined, particularly for representations like \textbf{10}, \textbf{15}, and \textbf{24} starting from the \textbf{5} representation.
  • Another participant suggests consulting chapter 18 of "Lie algebras in particle physics" by Georgi for further insights on the topic.
  • A later reply indicates an interest in understanding the motivation behind specific components of the decomposition, particularly questioning why the \textbf{5} representation must incorporate SU(2) × U(1) rather than SU(3) × SU(2) × U(1).
  • Further inquiry is made regarding whether the multiplets referenced in the text are indeed subgroups of SU(3) × SU(2) × U(1), indicating a potential misunderstanding or need for clarification on the relationships between these groups.

Areas of Agreement / Disagreement

Participants express varying levels of understanding and confusion regarding the decomposition process and the specific group structures involved. No consensus is reached on the motivations or requirements for the inclusion of certain groups in the decomposition.

Contextual Notes

Participants reference specific equations and chapters from literature, indicating that the discussion may depend on particular definitions and interpretations of group theory concepts. The motivations for choosing specific gauge groups in the decomposition remain unresolved.

Anchovy
Messages
99
Reaction score
2
When reading about GUTs you often come across the 'Standard Model decomposition' of the representations of a given gauge group. ie. you get the Standard Model gauge quantum numbers arranged between some brackets. For example, here are a few SM decompositions of the SU(5) representations \textbf{5}, \textbf{10}, \textbf{15} and \textbf{24}.

SU(5)_SM_decompositions.png


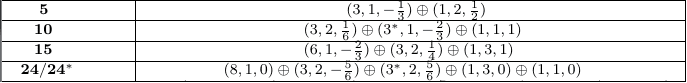
So, for instance this is telling us that the representation \textbf{5} will contain fields that are either

(SU(3)_{C} triplet, SU(2)_{L} singlet, hypercharge \tfrac{1}{2}Y = -\tfrac{1}{3}) for the (3, 1, -\tfrac{1}{3}),

or

(SU(3)_{C} singlet, SU(2)_{L} doublet, hypercharge \tfrac{1}{2}Y = \tfrac{1}{2}) for the (1, 2, \tfrac{1}{2}).

That's straightforward enough. However, I can't seem to find anything online explaining how these have been determined. I can find plenty about how you might go about constructing the \textbf{10}, \textbf{15} and \textbf{24} starting from combinations of the fundamental \textbf{5} by the 'Young's Tableaux' method, but nothing about starting with one of these SU(5) representations and breaking them down. Can anyone explain or link to an explanation?
 
Physics news on Phys.org
Try chapter 18 of "Lie algebras in particle physics" by Georgi.
 
Andrea M. said:
Try chapter 18 of "Lie algebras in particle physics" by Georgi.

OK, found a pdf version, will check it out very soon.
 
I'm wondering something about what it says here. Specifically I am trying to understand the motivation for the part that's in the red box. I have also highlighted earlier parts in green boxes that I suspect might be related, but I don't quite understand.

SU(5)_SM_decompositions__Georgi_book.png


So it wants to get the SM decomposition of the \textbf{5} by choosing from constituents of the equation (18.13) that combine to form a 5-dimensional subset. Fair enough. What I don't understand is the SU(2) \times U(1) part. Why must the \textbf{5} incorporate that specifically? Why not require, say, SU(3) \times SU(2) \times U(1)?
 
Anchovy said:
Why must the 5\textbf{5} incorporate that specifically? Why not require, say, SU(3)×SU(2)×U(1)SU(3) \times SU(2) \times U(1)?

The multiplets in ##(18.15)## aren't a subgroups of ##SU(3)\times SU(2)\times U(1)##?
 

Similar threads

Graduate SU(5), 'Standard Model decomposition', direct sum etc.
  • · Replies 23 ·
Replies
23
Views
5K
Graduate How can the LRS model for leptons incorporate the Standard Model group?
  • · Replies 4 ·
Replies
4
Views
2K
Graduate How many generations and fermions are there in the Standard Model Group?
  • · Replies 2 ·
Replies
2
Views
2K
High School Graphical representation of the weak mixing angle
  • · Replies 12 ·
Replies
12
Views
3K
Graduate Three dimensional representation of ##U(1)\times SU(2)##
  • · Replies 6 ·
Replies
6
Views
2K
Graduate Covariant derivative in Standard Model
  • · Replies 1 ·
Replies
1
Views
3K
Graduate Breaking of ##SU(2) \times SU(2)## to ##SU(2)##
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Standard Model SU(2) singlets and doublets
  • · Replies 2 ·
Replies
2
Views
4K
Graduate Why Is the Mixed SU(2) Term Invariant in Scalar Multiplet Models?
  • · Replies 2 ·
Replies
2
Views
4K
Graduate Why are particles in low representations in the Standard Model?
  • · Replies 6 ·
Replies
6
Views
1K