Statics - finding a moment of a force in xyz plane

[yugeci]

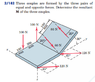
Homework Statement

I attached the question.

Homework Equations

M = r x F
M = F x d
Resolving forces, Fx/Fy/Fz = F cos/sin theta (depending on which angle you take)

The Attempt at a Solution

I can easily find the moment of the 100 N and 120 forces, but I'm having trouble finding the moment of the 80 N force. I know we use r x F, but getting the r and F vectors is a problem for me. Here is my attempt:

Fx = -80 cos 20 = -75.18
Fy = 80 sin 20 cos 60 = 13.68
Fz = 80 sin 20 sin 60 = 23.70

F = (-75.18i + 13.68j + 23.70k)

Rx = 0, to get Ry and Rz I made a triangle with the 180mm length and 30 degree angle.

Ry = 180 cos 30 = 155.88
Rz = -180 sin 30 = -90

R = (0, 155.88, -90)

M = r x F

When I take the cross product I get = { 4923.9972, 6766.2, 11719.0584 }

While the actual answer is { 0, -6770, 1172 }

Where did I make the mistake?

 

[dauto]

Your vector R seems incorrect. It is easier if you remember that the torque is perpendicular to the plane formed by F and R. find the unit vector perpendicular to the plane and multiply it by the magnitude of the torque.

 

[yugeci]

Your vector R seems incorrect. It is easier if you remember that the torque is perpendicular to the plane formed by F and R.

I had a feeling my R vector was wrong.. how would you calculate it correctly with the method I did then? I thought resolving the 180mm into y and z components would do it.

find the unit vector perpendicular to the plane and multiply it by the magnitude of the torque.

This seems to be what the solution says.

M2 = 80(0.180 cos 20) (-j sin 30 - k cos 30)

My question is, for the torque aren't the force and distance supposed to be perpendicular? If so how can you write 80(0.180 cos 20)? The force would be along the x-axis, but the 180mm length doesn't look perpendicular to it.

 

[dauto]

You method should work too. I think you just got some of the components with the wrong sign.

 

[haruspex]

My question is, for the torque aren't the force and distance supposed to be perpendicular? If so how can you write 80(0.180 cos 20)? The force would be along the x-axis, but the 180mm length doesn't look perpendicular to it.

That's what the cos(20) is for. The perpendicular distance is 0.180 cos (20); or, equivalently, the component of the 80 force perpendicular to the 0.18 measurement is 80 cos 20.