Statics: load supported on a wooden frame

Click For Summary

Discussion Overview

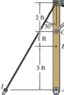
The discussion revolves around determining the internal loadings at point D of a wooden frame structure. Participants are analyzing the equilibrium equations and moment calculations related to the frame, exploring both theoretical and practical aspects of statics in engineering.

Discussion Character

  • Homework-related
  • Mathematical reasoning
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant presents a series of equilibrium equations to find the internal loadings, noting discrepancies in their calculations.
  • Another participant questions the direction of tension in the system, suggesting a need for consistent sign conventions in the equations.
  • A participant acknowledges a mistake in their calculations and corrects the tension direction for IB, while questioning the correctness of their assumptions about Ay and the forces acting on the frame.
  • There is a discussion about the moment calculations around different points (I and D) and how they relate to the values of GH and IB.
  • One participant suggests that an error may lie in the logic rather than the math when calculating GH from the y-direction forces.
  • Another participant points out a potential double counting issue in the forces being considered, emphasizing the need to differentiate between forces at different points in the frame.

Areas of Agreement / Disagreement

Participants express differing views on the correctness of the calculations and assumptions made regarding the forces and moments in the frame. There is no consensus on the correct approach or final values, as multiple interpretations and corrections are presented.

Contextual Notes

Participants highlight potential limitations in their calculations, including assumptions about force directions, the impact of geometry on force components, and the need for careful consideration of equilibrium conditions. The discussion reflects ongoing refinement of ideas rather than settled conclusions.

Who May Find This Useful

This discussion may be useful for students and practitioners in engineering and physics who are grappling with concepts of statics, equilibrium, and internal load analysis in structural systems.

SoylentBlue
Messages
50
Reaction score
8

Homework Statement


Given the frame shown, determine the internal loadings at D

Homework Equations

The Attempt at a Solution


This should be a simple problem...but I cannot see where I am making a mistake.
If I approach it by examining the entire structure, I get a wrong answer:

ΣFx: Ax + (cos60)IB = 0
ΣFy: Ay - (sin60)IB – 150 = 0
ΣM about I I: 3.44Ay – (7.44)(150) = 0

The 3.44 comes from determining, by trig, that IA is 3.44; the 150LB load is therefore 7.44 ft away from I

This yields Ay = 324.4
Plug back into sum of forces in y-direction; that yields IB = -201

OK now examine the section BDHC:
ΣFx: -(cos60)(201) + (cos45)GH=0
This yields GH= 142, which is wrong.
___________________

However, if I start instead with just the structure BDHC, I get:
sum of moments about B: (2)[(sin45)GH] – (4)(150)=0 then GH=424 which agrees with the book

Where did I make a wrong turn? Any help greatly appreciated. Thank you.:smile:

[/B]
 

Attachments

  • Prob1-15A.jpg
    Prob1-15A.jpg
    8.2 KB · Views: 449
  • Prob1-15ABI.jpg
    Prob1-15ABI.jpg
    4.3 KB · Views: 394
  • Prob1-15BDHC.jpg
    Prob1-15BDHC.jpg
    2.5 KB · Views: 374
Physics news on Phys.org
SoylentBlue said:
ΣFx: Ax + (cos60)IB = 0
Which way is the tension IB acting on the system? Have you been consistent with signs?
 
IB would have to be in tension. So at point I, Ix is to the left, and Iy is negative.

Oh, I see your point. Let's amend the equation:
ΣFx: Ax - (cos60)IB = 0
However, for the Fy equation, which is where we determine the value of Ay, the signs and logic and values are correct, right?
I assume Ay goes up, and AB is in compression. Obviously, the load goes down. And IB is in tension, so Iy goes down.

Small typo I just noticed...this should read:
ΣM about point I: 3.44Ay – (7.44)(150) = 0

Thank you for helping...I am trying to work through this course on my own, so the Internet is my instructor!:smile:
 
SoylentBlue said:
This yields Ay = 324.4
Plug back into sum of forces in y-direction; that yields IB = -201
Try that step again. I get a positive IB (as it should be).
 
Now that was an embarrassing error.:oops: OK, I now have the correct answer for IB.

Next, we look at the top of the frame, examining DHC; If we sum the moments from point D, the moment caused by GH balances the moment caused by the load at point C, and we get the correct answer for the value of GH. So far so good.

However, shouldn't we also be able to look at BDHC, and sum all the forces in either the x or y direction? If we look at the y direction, in that case we get an incorrect value of zero for GH.
ΣFy: Ay - (cos30)(IB) + (cos45)(GH) -150=0
Ay is in compression, pushing up; IB is in tension pulling down, GH is pushing up, and of course the 150 load pulls down.
324 - 174+.707GH-150=0
324-324 = .707GH

This has to be an error in logic rather than a math error, right?
 

Attachments

  • prob115BDHC.jpg
    prob115BDHC.jpg
    2.9 KB · Views: 331
SoylentBlue said:
If we sum the moments from point D, the moment caused by GH balances the moment caused by the load at point C
I assume you meant moments about B.
SoylentBlue said:
Ay - (cos30)(IB) + (cos45)(GH)
You are double counting.
The vertical force in AB is not the same all the way up. The force at A includes a component to balance the vertical load at G from GH. The force in AB at B does not include this. If your Ay is the force at A then you should not add a contribution from GH at H.
 

Similar threads

Calculating Axle Loads for a Firefighter Vehicle: A Statics Problem
  • · Replies 13 ·
Replies
13
Views
12K