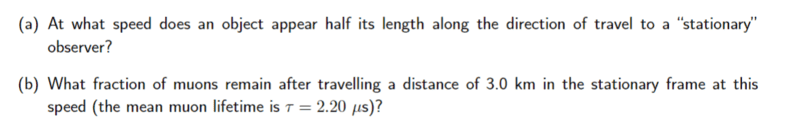SUMMARY
The discussion centers on the concept of a "stationary observer" in the context of special relativity. Participants clarify that "stationary" refers to an observer's rest frame, which is inertial, and does not require another object to be at rest. The conversation also delves into a specific problem involving length contraction, where one participant struggles with deriving the correct relationship between length and velocity, ultimately realizing a sign error in their algebraic manipulation. The importance of showing all algebraic steps to avoid confusion is emphasized.
PREREQUISITES
- Understanding of special relativity concepts, particularly length contraction
- Familiarity with the Lorentz factor (γ)
- Basic algebra skills for manipulating equations
- Knowledge of inertial reference frames
NEXT STEPS
- Study the derivation of the Lorentz transformation equations
- Learn about the implications of length contraction in different inertial frames
- Explore examples of algebraic manipulation in physics problems
- Review the concept of inertial versus non-inertial reference frames
USEFUL FOR
Students and educators in physics, particularly those studying special relativity, as well as anyone interested in understanding the nuances of observer frames and algebraic problem-solving in physics.