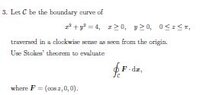Step-by-Step Guide to Overcoming Inexperience: Help for Beginners

  • Context: MHB 
  • Thread starter Thread starter Doomknightx9
  • Start date Start date
Click For Summary
SUMMARY

This discussion focuses on providing a structured approach for beginners to overcome inexperience in complex topics. It emphasizes the importance of self-directed learning by encouraging individuals to identify and research unfamiliar concepts, such as Stokes' theorem. The conversation highlights the necessity of breaking down questions into manageable parts and seeking clarity through independent investigation. This method fosters a deeper understanding and builds confidence in tackling challenging subjects.

PREREQUISITES
  • Basic understanding of calculus concepts
  • Familiarity with vector calculus
  • Knowledge of mathematical theorems
  • Ability to conduct independent research
NEXT STEPS
  • Research Stokes' theorem and its applications in physics and engineering
  • Explore resources on vector calculus fundamentals
  • Learn techniques for effective independent study and research
  • Investigate common mathematical theorems and their proofs
USEFUL FOR

Students, educators, and anyone seeking to enhance their understanding of advanced mathematical concepts and improve their self-learning strategies.

Doomknightx9
Messages
2
Reaction score
0
I have no idea how to do this. Can i get some steps and a solution please
 

Attachments

  • dd.JPG
    dd.JPG
    4.5 KB · Views: 109
Physics news on Phys.org
Surely you don't have no idea. Try reading through the question and every time you come across something you aren't sure about, jot it down and investigate it independently. For example, what is Stokes' theorem? What does it say and when do we use it?
 

Similar threads

Undergrad Could anyone give me a step by step guide to using VASP for DFT calculations?
  • · Replies 3 ·
Replies
3
Views
649
MHB Trouble finding the derivative of a fraction using four step process
  • · Replies 2 ·
Replies
2
Views
2K
MHB Solve ln(x-1)/x-3=2 | Step-by-Step Guide
  • · Replies 6 ·
Replies
6
Views
3K
Undergrad Explicit logical justification for last step in epsilon/delta proof?
  • · Replies 20 ·
Replies
20
Views
2K
MHB Using advanced calculus for finding values
  • · Replies 2 ·
Replies
2
Views
1K
MHB Math Trick: How to Turn 1/25 Into 10 - Step by Step Guide
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Integral confusion for a simple Differential Equation
  • · Replies 2 ·
Replies
2
Views
1K
MHB Understanding Curve Sketching for a Challenging Function
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Robert Adams textbook: Acceleration example
  • · Replies 7 ·
Replies
7
Views
2K
Graduate The partial derivative of a function that includes step functions
  • · Replies 3 ·
Replies
3
Views
4K