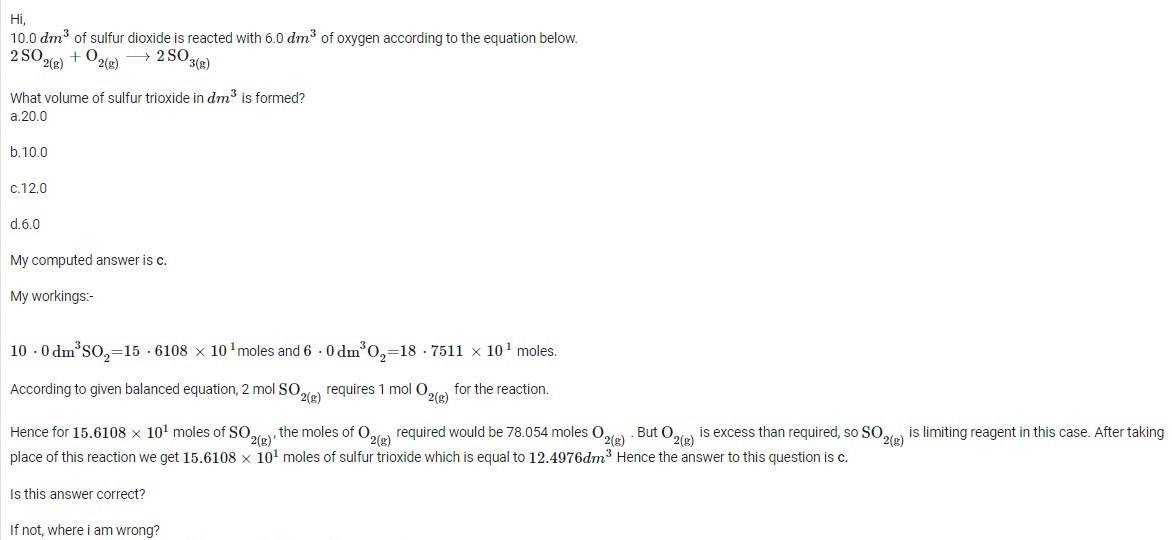SUMMARY
The discussion centers on a stoichiometry question regarding gas volumes during a chemical reaction. It establishes that the volume of a gas at standard pressure and temperature (STP) is determined by the number of molecules, leading to the conclusion that the volume of sulfur trioxide ($\ce{SO3(g)}$) remains at $10.0\,\text{dm}^3$ after the reaction. The initial volumes of sulfur dioxide ($\ce{SO2(g)}$) and oxygen ($\ce{O2(g)}$) are $10.0\,\text{dm}^3$ and $6.0\,\text{dm}^3$, respectively, with only $5.0\,\text{dm}^3$ of oxygen being consumed. This confirms the principle of gas volume conservation in stoichiometric reactions.
PREREQUISITES
- Understanding of stoichiometry principles
- Knowledge of gas laws, particularly at standard temperature and pressure (STP)
- Familiarity with the concept of molar volume ($V_m$)
- Basic chemical reaction balancing skills
NEXT STEPS
- Study the Ideal Gas Law and its applications in stoichiometry
- Learn about molar volume calculations at STP
- Explore advanced stoichiometric calculations involving multiple reactants and products
- Investigate the impact of temperature and pressure changes on gas volumes
USEFUL FOR
Chemistry students, educators, and professionals involved in chemical engineering or laboratory work who require a solid understanding of gas behavior in stoichiometric reactions.