SUMMARY
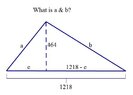
The discussion revolves around solving for the sides 'a' and 'b' of a triangle given its height and base, specifically using the Pythagorean theorem and the Geometric Mean Theorem. The equations presented are $$464^2 + e^2 = a^2$$ and $$464^2 + (1218 - e)^2 = b^2$$, alongside the equation $$464^2 = e \cdot (1218 - e)$$. The problem involves three unknowns: 'a', 'b', and 'e', with the goal of determining their values and confirming if the angle between 'a' and 'b' is 90 degrees.
PREREQUISITES
- Understanding of the Pythagorean theorem
- Familiarity with the Geometric Mean Theorem
- Basic knowledge of right triangles
- Ability to solve systems of equations
NEXT STEPS
- Study the application of the Pythagorean theorem in triangle problems
- Explore the Geometric Mean Theorem in more depth
- Learn methods for solving systems of nonlinear equations
- Investigate properties of right triangles and their angles
USEFUL FOR
Mathematicians, geometry students, and anyone involved in solving triangle-related problems will benefit from this discussion.