Badre
- 11
- 0
This problem has been posted here a couple of times, but I can't finish it off, due to some combination of my failure to sum the torques and working out the geometry.
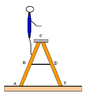
A student is standing on a ladder as shown in the figure to the right. Each leg of the ladder is 2.7 m long and is hidged at point C. The tie-rod (BD) attached halfway up and is 0.72 m long. The student is standing at a spot 2.025 m along the leg and her weight is 466 N. (You may ignore the weight of the ladder and any minor friction between the floor and the legs.)
Sum of Forces = 0
Sum of Torques = 0
W = weight of student
T = Tension
Nl = Normal force at point A on left leg
Nr = Normal force at point E on right leg
Cr, Cl = The forces exerted on the ladder legs by each other respectively at point C.
I started by calculating θ (the angle at a) as sin θ = .36/1.35. Is this the proper way to do this? I'm not sure if I can say that the length of the ladder leg is 1.35 halfway up the vertical height. I found θ=74.534
I then summed torques about point C.
(T(2.7/2)sin θ) - (W(2.025)cos θ) - (Nl(2.7)cos θ) = 0
Nl = 1.8071T - 349.5
I then plugged this equation into
T-Clx = 0 and Cly + Nl - W = 0
in an attempt to solve for T, but am unable to get the correct answer.
I'm not sure if I've set up the torque equation properly or if I've performed the trigonometry correctly to find the angles. I'd greatly appreciate any guidance here.
Homework Statement
A student is standing on a ladder as shown in the figure to the right. Each leg of the ladder is 2.7 m long and is hidged at point C. The tie-rod (BD) attached halfway up and is 0.72 m long. The student is standing at a spot 2.025 m along the leg and her weight is 466 N. (You may ignore the weight of the ladder and any minor friction between the floor and the legs.)
Homework Equations
Sum of Forces = 0
Sum of Torques = 0
W = weight of student
T = Tension
Nl = Normal force at point A on left leg
Nr = Normal force at point E on right leg
Cr, Cl = The forces exerted on the ladder legs by each other respectively at point C.
The Attempt at a Solution
I started by calculating θ (the angle at a) as sin θ = .36/1.35. Is this the proper way to do this? I'm not sure if I can say that the length of the ladder leg is 1.35 halfway up the vertical height. I found θ=74.534
I then summed torques about point C.
(T(2.7/2)sin θ) - (W(2.025)cos θ) - (Nl(2.7)cos θ) = 0
Nl = 1.8071T - 349.5
I then plugged this equation into
T-Clx = 0 and Cly + Nl - W = 0
in an attempt to solve for T, but am unable to get the correct answer.
I'm not sure if I've set up the torque equation properly or if I've performed the trigonometry correctly to find the angles. I'd greatly appreciate any guidance here.