- 20,815
- 28,445
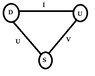
If we consider the generators of SU(3) in the standard model. Is there a direct correspondence between them and a physical quantity, esp. if we only consider ##T_+=\frac{1}{2}(\lambda_1+i\lambda_2)\; , \;U_+=\frac{1}{2}(\lambda_6+i\lambda_7)\; , \;V_+=\frac{1}{2}(\lambda_4+i\lambda_5)##, do they directly represent a quantity? And what does ##V_+## stand for?