Sum and Product of Real Roots of A Quartic Function

[anemone]

Let $p$ be the sum and $q$ be the product of all real roots of the equation $x^4-x^3-1=0$.

Prove that $q<-\dfrac{11}{10}$ and $p>\dfrac{6}{11}$.

 

[juantheron]

Let $f(x) = x^4-x^3-1$, Now $f^{'}(x) = 4x^3-3x^2 = x^2\cdot (4x-3)$

Now for Max. or Min., $f^{'}(x) = 0\Leftrightarrow x^2\cdot (4x-3) = 0$

So $\displaystyle x = 0\;\;,\frac{3}{4}$ (Here $x= 0 $ is called point of inflection because $f^{''}(x) = 0$)

Now we will check where function is Strictly Increasing and where Strictly decreasing.

So for $\displaystyle x<\frac{3}{4},$ function is strictly decreasing.

and for $\displaystyle x>\frac{3}{4},$ function is strictly Increasing.

and $f(-1) = 1>0$ and $f(0) = -1<0$ and $f(1) = -1$ and $f(2) = 7>0$

So using IMVT, The given equation has only two real roots,

one lie between $\left(-1,0\right)$ and other lie between $\left(1,2\right)$

Now we will find some nearset upper and lower bound for both roots for achieving the given inequality.

but I did not found here (struck here)

Thanks

 

[anemone]

Let $p$ be the sum and $q$ be the product of all real roots of the equation $x^4-x^3-1=0$.

Prove that $q<-\dfrac{11}{10}$ and $p>\dfrac{6}{11}$.

Thanks for participating, jacks and thanks for the thought!

Yes, if we let $y=x^4-x^3-1=0$, the function of $y$ has two real roots based on the first and second derivative tests since

1.

$$\frac{dy}{dx}=x^2(4x-3)$$ and this tells us $y$ increases for $$x>\frac{3}{4}$$ and decreases for $$x<\frac{3}{4}$$ and also, there are two critical points which occur at $x=1$ and $x=\dfrac{3}{4}$

2.

$$\frac{d^2y}{dx^2}=3x(4x-1)$$ and this tells us $x=1$ is an inflexion point and there is a minimum point which occurs at $$x=\frac{3}{4}$$.

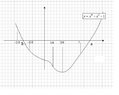
Here is the rough sketch of the graph of the function of $y=x^4-x^3-1$.

View attachment 1543

If we let $a, b$ where $a>0$ and $b<0$ to represent the two real roots of the function of $y$, we know we must have

[TABLE="class: grid, width: 500"]
[TR]
[TD]$m<a<n$ and[/TD]
[TD]$-j<b<-k$ where $j,k>0$.[/TD]
[/TR]
[TR]
[TD]where $ab=q<-mk=-\dfrac{11}{10}$ and[/TD]
[TD]$a+b>m-j=\dfrac{6}{11}$.[/TD]
[/TR]
[/TABLE]

And after a few attempts to guess the four values for $m, n, j, k$, we see that one of the possible combinations of them would be

[TABLE="class: grid"]
[TR]
[TD]$f(\dfrac{11}{8})=(\dfrac{11}{8})^4-(\dfrac{11}{8})^3-1=-0.025$

and

$f(\dfrac{7}{5})=(\dfrac{7}{5})^4-(\dfrac{7}{5})^3-1=0.0976$[/TD]
[TD]$f(-\dfrac{73}{88})=(-\dfrac{73}{88})^4-(-\dfrac{73}{88})^3-1=0.04439$

and

$f(-\dfrac{4}{5})=(-\dfrac{4}{5})^4-(-\dfrac{4}{5})^3-1=-0.0784$[/TD]
[/TR]
[TR]
[TD]$\dfrac{11}{8}<a<\dfrac{7}{5}$ and[/TD]
[TD]$-\dfrac{73}{88}<b<-\dfrac{4}{5}$[/TD]
[/TR]
[TR]
[TD]where $ab=q<-mk=-\dfrac{11}{10}$ and[/TD]
[TD]$a+b>m-j=\dfrac{6}{11}$.[/TD]
[/TR]
[/TABLE]

and these give us

$ab=q<-\dfrac{11}{8}\dfrac{4}{5}=-\dfrac{11}{10}$,

$a+b=p>\dfrac{11}{8}-\dfrac{73}{88}=\dfrac{6}{11}$ and hence, we're done with the proof.

By the way, below are the attempts which lead me to the final guess of the all four values of $m, n, j, k$.
[TABLE="class: grid, width: 500"]
[TR]
[TD]$0.9<a<?$

$-?<b<-\dfrac{11}{9}$[/TD]
[TD]$1.2<a<?$

$-?<b<-\dfrac{11}{12}$[/TD]
[/TR]
[/TABLE]