Re: Subshine's questions at Yahoo! Answers regarding solids of revolution
Hello sunshine,
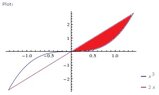
a) Here is a graph of the region $R$ to be revolved about the $x$-axis:
View attachment 899
We may revolve the area shaded in red and then double the volume to find the requested volume.
The volume of an arbitrary washer is:
$$dV=\pi\left(R^2-r^2 \right)\,dx$$
where:
$$R=2x$$
$$r=x^3$$
and so we have:
$$dV=\pi\left((2x)^2-\left(x^3 \right)^2 \right)\,dx=\pi\left(4x^2-x^6 \right)\,dx$$
To determine the limits of integration, we may equate the two functions:
$$x^3=2x$$
$$x\left(x^2-2 \right)=0$$
$$x=0,\,\pm2$$
Hence, summing the disks by integrating, we find:
$$V=2\pi\int_0^{\sqrt{2}}4x^2-x^6\,dx=2\pi\left[\frac{4}{3}x^3-\frac{1}{7}x^7 \right]_0^{\sqrt{2}}=\frac{16\sqrt{2}\pi}{21}\left(7-3 \right)=\frac{64\sqrt{2}\pi}{21}$$
Now, whenever possible, I like to use the shell method to check my work.
The volume of an arbitrary shell is:
$$dV=2\pi rh\,dy$$
where:
$$r=y$$
$$h=y^{\frac{1}{3}}-\frac{y}{2}$$
and so we have:
$$dV=2\pi y\left(y^{\frac{1}{3}}-\frac{y}{2} \right)\,dy=2\pi\left(y^{\frac{4}{3}}-\frac{y^2}{2} \right)\,dy$$
To determine the limits of integration, we may equation the two functions:
$$y^{\frac{1}{3}}=\frac{y}{2}$$
$$y-2y^{\frac{1}{3}}=0$$
$$y^{\frac{1}{3}}\left(y^{\frac{2}{3}}-2 \right)$$
$$y=0,\,\pm2\sqrt{2}$$
Thus, summing the shells by integration we find:
$$V=4\pi\int_0^{2\sqrt{2}}y^{\frac{4}{3}}-\frac{y^2}{2}\,dy=4\pi\left[\frac{3}{7}y^{\frac{7}{3}}-\frac{1}{6}y^3 \right]_0^{2\sqrt{2}}=\frac{16\sqrt{2}\pi}{21}\left(18-14 \right)=\frac{64\sqrt{2}\pi}{21}$$
This checks with the result we obtained using the washer method.
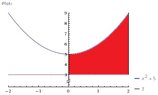
b) Here is a graph of the region $R$ to be revolved about the $y$-axis:
View attachment 900
We need only revolve the area shaded in red to find the requested volume.
Using the disk/washer method, we should observe that for $3\le y\le5$ we simply have a right circular cylinder of radius 2 and height 2, hence:
$$V_1=\pi(2)^22=8\pi$$
To find the remaining volume, we may use the washer method. The volume of an arbitrary washer is:
$$dV_2=\pi\left(R^2-r^2 \right)\,dy$$
where:
$$R=2$$
$$r=\sqrt{y-5}$$
and so we have:
$$dV_2=\pi\left((2)^2-\left(\sqrt{y-5} \right)^2 \right)\,dy=\pi\left(9-y \right)\,dy$$
Summing the washers by integration, we find:
$$V_2=\pi\int_5^9 9-y\,dy=\pi\left[9y-\frac{1}{2}y^2 \right]_5^9=\frac{\pi}{2}\left(\left(2\cdot9^2-9^2 \right)-(90-25) \right)=8\pi$$
Thus, the total volume is:
$$V=V_1+V_2=8\pi+8\pi=16\pi$$
Now, using the shell method to check our work, we find the volume of an arbitrary shell is:
$$dV=2\pi rh\,dx$$
where:
$$r=x$$
$$h=x^2+5-3=x^2+2$$
and so we have:
$$dV=2\pi x\left(x^2+2 \right)\,dx=2\pi\left(x^3+2x \right)\,dx$$
Summing the shells by integrating, we find:
$$V=2\pi\int_0^2 x^3+2x\,dx=2\pi\left[\frac{1}{4}x^4+x^2 \right]_0^2=2\frac{\pi}{2}\left(2^4+2^4 \right)=16\pi$$
This checks with our previous result.