Superdense coding for sending 2 qubits at a time?

[Strilanc]

[Superdense coding](http://en.wikipedia.org/wiki/Superdense_coding) is a way to send 2 classical bits by sending only 1 qubit and 'consuming' a previously shared entangled qubit. (Normally you could only send 1 classical bit per qubit.)

My question is: why doesn't this work (or does it?) for sending two qubits packed using a single sent qubit and the pre-entangled qubit?

Here's a quantum circuit that does superdense coding:

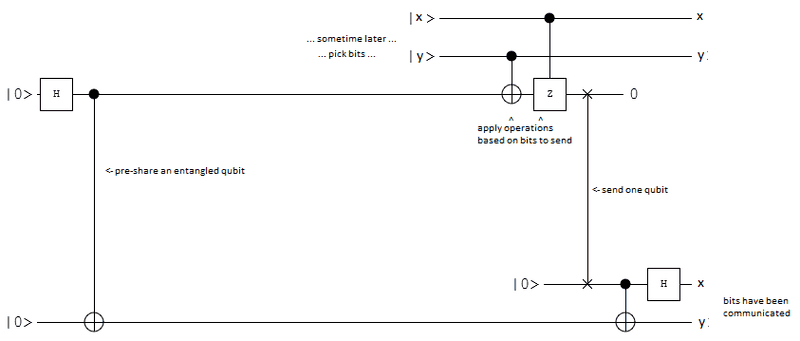
It starts by Alice (top) and Bob (bottom) sharing a bell pair. Then, later, Alice chooses two bits to send. She applies X and Z gates to her half of the pair conditionally based on those bits, then send it. Bob then cnot's it into the half he already had, and Hadamard's it. Now Bob has the two bits Alice chose.

Ignoring the fact that this is amazing because it let's you store bandwidth, shouldn't it also work for qubits instead of just classical bits? From what I can tell, if x and y are in superposition then at the end Alice and Bob are in a superposition where their bits always match. Even if x and y are entangled with some other stuff.

You can experiment with this circuit by going to this online simulator and pasting the following json (Workspace -> Import JSON):

{"gates":[],"circuit":[{"type":"h","time":0,"targets":[2],"controls":[]},{"type":"x","time":1,"targets":[8],"controls":[2]},{"type":"h","time":5,"targets":[4],"controls":[]},{"type":"h","time":5,"targets":[0],"controls":[]},{"type":"h","time":5,"targets":[1],"controls":[]},{"type":"x","time":6,"targets":[0],"controls":[4]},{"type":"x","time":12,"targets":[2],"controls":[1]},{"type":"z","time":13,"targets":[2],"controls":[0]},{"type":"swap","time":14,"targets":[2,7],"controls":[]},{"type":"x","time":15,"targets":[8],"controls":[7]},{"type":"h","time":16,"targets":[7],"controls":[]}],"qubits":9,"input":[0,0,0,0,0,0,0,0,0]}

Note that I added a few gates to place the bits into superposition. Notice that if you evaluate the circuit the last two and first two bits always match within the superposition. Does that mean I can consume an entangled qubit to send two entangled qubits as one?

... Maybe it's the fact that the qubits are not communicated, in that they end up entangled instead of (impossibly) cloned?

 

[Strilanc]

After having thought about this more I'm come to the conclusion that my hunch mentioned at the end is right. The reason you can't use it to send qubits, despite being able to send superpositions of classical bits, is that Alice still has an entangled copy of the same superposition. So if Bob tries to do fancy stuff with his qubits (like superdense coding), it will fail to work because Alice's stuff prevents the appropriate components from interfering.

It might be possible to get around this, by cancelling her information (e.g. two CNOTs back from Bob to Alice), but I don't think there's a way to do it that keeps the speedup.