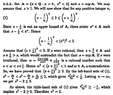MI6
The following is my book's proof that $\sup\left\{x\in\mathbb{Q}:x>0, ~ x^2<2\right\} = \sqrt{2}.$
http://www.mathhelpboards.com/attachment.php?attachmentid=527&d=1356865161
I don't follow the bit where it says "if s were irrational, then w = \frac{\lfloor(n+1)s\rfloor}{n+1}+\frac{1}{n+1}."
Could someone please elaborate on that bit? How does s being irrational imply that?
http://www.mathhelpboards.com/attachment.php?attachmentid=527&d=1356865161
I don't follow the bit where it says "if s were irrational, then w = \frac{\lfloor(n+1)s\rfloor}{n+1}+\frac{1}{n+1}."
Could someone please elaborate on that bit? How does s being irrational imply that?
Attachments
Last edited by a moderator: