Surface speed of a strip over a deflection roll

[omega_minus]

TL;DR

A question on roll speed with compressible material deflecting over its surface

Hello,
I am trying to solve a problem at work that at first I thought was easy but has proven trickier than I originally thought:

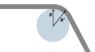
If I have a strip of material traveling in a straight line and it is tangent to a roll turning below it, the roll would need to turn at the surface speed of the material to avoid it skidding. The speed is simply v=rw, where v is the strip linear speed, r is the radius of the roll and w is the rotational velocity (in radians/sec). However, if the material bends at the roll (deflection) I am not so sure about the relationship. (See attached image)

Consider that the material is rather thick. As is deflects there is an inner and outer radius of the material. I'd think the material (steel in this case) must compress on the inner radius and stretch on the outer surface. This means now the underside and top side are moving at different rates. If the material is not to skid (not to move relative to the surface of the roll), what speed should the roll turn if the incoming strip speed remains fixed?

My initial thought is that it turns at the speed given by the previous relation. But different "layers" of the compressing/stretching strip are moving at different velocities (strip velocity plus or minus the stretching and compressing rates). So if the roll turns at the speed of the surface layer there'd be an instantaneous jump in roll speed for any deflection whatsoever that wouldn't seem to be a function of wrap angle. This is counterintuitive (but that doesn't mean it can't be right). I have also considered that the strip could only be stationary to the roll's surface at one point since the underside compresses coming in and must then stretch out again on leaving the deflection roll. But this doesn't help me to see the answer either.

Can anyone give me an idea of how to solve this problem? I've searched all over google and the forums but I may not be looking with the best search terms.
Thanks

 

[jrmichler]

The sheet metal forming people have studied this problem in depth. Dissertations have been written on the subject. This one, for example: The Drawbead as a Control Element in Sheet Metal Forming, a copy of which is in the Michigan Tech library (mtu.edu).

The figure below shows what is happening:

The strip arrives at the roll with a velocity. That velocity is constant over the entire thickness of the strip. At the tangent point on the roll where the strip first touches the roll, it bends. The region where bending occurs is shaded. After bending, the strip is a circular arc, with velocity R * omega, where:

R is the distance from the center of the roll
Omega is the angular velocity of the roll

The neutral axis of the strip after bending is moving at the same velocity as the portion of strip before the roll. The location of the neutral axis is not the centerline of the strip because it depends on the front and back tension in the strip. At the tangent point where the strip leaves the roll, it unbends. Note that "bend" and "unbend" are correct terms in the sheet metal forming field. This discussion assumes that the strip is not slipping against the roll, and also that the front and back tensions are enough to form the strip to the roll.

Since the strip is bent and unbent under tension, the length, and thus the thickness, can change. If the length changes, the leaving velocity will be higher than the entering velocity. The exact roll RPM will be dependent on the exact location of the neutral axis of the bent sheet metal. And the location of the neutral axis is a result of yield stress, front tension, and back tension. So you will not know the roll RPM exactly. Approximately, but not exactly.

Note also that significant work is being done to the strip to bend and unbend it. That work is provided by a difference between front and back tension, plus the torque to drive the roll.

This is a web handling problem, where the web is both strong and longitudinally stiff. The control scheme for the roll drive must be selected accordingly.

Bonus points if you borrow a copy of that dissertation via interlibrary loan and actually read it.

 

[omega_minus]

The sheet metal forming people have studied this problem in depth. Dissertations have been written on the subject. This one, for example: The Drawbead as a Control Element in Sheet Metal Forming, a copy of which is in the Michigan Tech library (mtu.edu).

The figure below shows what is happening:
View attachment 255533The strip arrives at the roll with a velocity. That velocity is constant over the entire thickness of the strip. At the tangent point on the roll where the strip first touches the roll, it bends. The region where bending occurs is shaded. After bending, the strip is a circular arc, with velocity R * omega, where:

R is the distance from the center of the roll
Omega is the angular velocity of the roll

The neutral axis of the strip after bending is moving at the same velocity as the portion of strip before the roll. The location of the neutral axis is not the centerline of the strip because it depends on the front and back tension in the strip. At the tangent point where the strip leaves the roll, it unbends. Note that "bend" and "unbend" are correct terms in the sheet metal forming field. This discussion assumes that the strip is not slipping against the roll, and also that the front and back tensions are enough to form the strip to the roll.

Since the strip is bent and unbent under tension, the length, and thus the thickness, can change. If the length changes, the leaving velocity will be higher than the entering velocity. The exact roll RPM will be dependent on the exact location of the neutral axis of the bent sheet metal. And the location of the neutral axis is a result of yield stress, front tension, and back tension. So you will not know the roll RPM exactly. Approximately, but not exactly.

Note also that significant work is being done to the strip to bend and unbend it. That work is provided by a difference between front and back tension, plus the torque to drive the roll.

This is a web handling problem, where the web is both strong and longitudinally stiff. The control scheme for the roll drive must be selected accordingly.

Bonus points if you borrow a copy of that dissertation via interlibrary loan and actually read it.

Well, thank you Dr. Michler. This is exactly the kind of answer I was hoping for. I couldn't access the paper through the university (yours or mine) but I requested the full text through ResearchGate before realizing it was actually your dissertation! Anyways, I'd really like to read it and I'm glad I wasn't stumped by a trivial problem. Thanks again for the valuable information and let me know if there is another way I can access the paper.

 

[Baluncore]

My answer is similar and inline with that above.

As a first approximation you might assume the thick sheet has a constant thickness, with a neutral axis plane. Assume the sheet only contacts the roller where it is following the cylindrical surface of the roller. The contact surface of the sheet will then decelerate at the instant it bends into contact with the roller. At the same instant, the outer surface will accelerate. The situation reverses on exit.
The radius of the roller is then effectively increased by half the sheet thickness.
So the physical roller should be reduced in radius by half the sheet thickness to compensate.
Or the roller should be slowed to match the inner radius velocity.

A second approximation will allow for lengthening of the sheet due to asymmetric plastic deformation caused by the biased sum of sheet tension and bending stress. That lengthening will result in a proportional thinning of the sheet.

'Tis a pity the JRM thesis is not available as a goodread.pdf on the web.

 

[omega_minus]

'Tis a pity the JRM thesis is not available as a goodread.pdf on the web.

I agree and thanks for your reply. Your first approximation is what I was thinking when I realized that the roll's diameter would "jump" by half the thickness. If the material was really thick this would be an obvious effect and what struck me as weird was that for zero deflection the strip speed would be the same everywhere. But for any deflection whatsoever (say one thousandth of a degree) the speed would instantly change to a value that would not depend on the deflection (wrap) angle. This kind of digital change in speed (and hence kinetic energy of a differential volume) would represent an infinite amount of power. That is, the change in energy would occur in zero time. This is clearly not possible. The OEM of our control scheme makes this approximation in our software and it was asked of me by another automation engineer if this was right. It seemed to us that it was not but I couldn't prove it mathematically.

 

[Baluncore]

This kind of digital change in speed (and hence kinetic energy of a differential volume) would represent an infinite amount of power. That is, the change in energy would occur in zero time. This is clearly not possible.

Then let's have a third level of approximation where the sheet is pulled onto the roller by tension from down stream. The bending of the sheet onto the roller will push the approaching sheet away from the roller, with the roller acting like a fulcrum. That bending wave will travel up-stream at the speed of a shear wave in the sheet material. The result will be a smooth transition onto the roller, starting before the sheet reaches the roller. The transition is then not instantaneous, and the force not infinite, because the sheet can in a sense, respond to the 'sound' of the roller ahead.

 

[jrmichler]

The bending and unbending zones have approximate length equal to the thickness of the sheet, which eliminates mathematical infinities. It also means that a minimum wrap angle (and minimum sheet tension) is needed before the bending and unbending zones are separated by bent sheet wrapping the roll.

That dissertation was written back in the dark ages of paper copies. One for me, two for the library, and one for University Microfilms.

 

[omega_minus]

Thanks Dr. Michler, I appreciate your and baluncore’s input. I feel I have a better idea of what’s going on and will use the title of your paper to search for similar research.

 

[jrmichler]

References 3-6 and 86 in the dissertation are relevant and enough to keep you busy for a while. The other references are mostly about friction and/or drawbeads. They are as follows:

3) Swift, H.W., "Plastic Bending Under Tension", Engineering, Vol. 166, Oct. 1, 1948, pp. 333-359.

4) Hill, R., "The Mathematical Theory of Plasticity", Clarendon Press, 1950, pp. 79-81, pp. 287-300.

5) Lange, K., Ed., "Bending", Handbook of Metal Forming, McGraw-Hill, 1985, pp. 19.1-19.17.

6) Dadras, P. and Majlessi, S.A., "Plastic Bending of Work Hardening Materials", ASME Paper No. 82-Prod-2.

86) Hosford, W.F. and Caddell, R.M., "Metal Forming, Mechanics and Metallurgy", Prentice-Hall, 1983.