- #1
- 14,362
- 7,841
- Homework Statement
- A cylinder with an initial radius ##r_0## rolls without slipping on a horizontal surface with speed ##v_0## when it encounters snow region, still horizontal. As it rolls, snow sticks onto the cylinder which makes its radius slowly increase. The amount of gathered snow is proportional to the distance the snow cylinder has traveled.
Find the linear speed of the cylinder as a function of distance.
- Relevant Equations
- ##\tau=\frac{dL}{dt}##
This is a spin-off of a similar problem posted here in which the cylinder gathers snow as it rolls down an incline. I think one has to understand the snow-gathering process before attempting the more complicated case. A horizontal surface makes that easy but because it is a different problem, I opted to post my thoughts on this on a separate thread.
Here I will adopt a dynamic approach and consider that the angular momentum of the cylinder relative to the point of contact is conserved because the surface can exert no torque. For the reader's convenience, I reproduce derivations of relevant equations taken from the post quoted above.
Let ##\beta=## the rate at which the cylinder gathers snow. It is expedient to define dimensionless parameter ##u=\dfrac{\beta s}{m_0}## and write
Mass of cylinder: ##m=m_0+\beta s=(1+u)m_0.##
Radius of cylinder
To find ##r(s)## consider adding to the cylinder mass ##dm## in the form of a cylindrical tube of thickness ##dr## and radius ##r##. Then $$\begin{align} & \beta~ds=dm=\rho dV=\rho(2\pi r)(dr)L=\frac{m_0}{\pi r_0^2~L}(2\pi r)( dr)L=\frac{m_0}{ r_0^2}2rdr \nonumber \\
&\implies \frac{m_0}{ r_0^2} \int_{r_0}^{r}2rdr = \beta \int_0^s ds \implies r^2=r_0^2\left(1+\frac{\beta s}{m_0} \right)\implies r=(1+u)^{1/2}r_0.
\nonumber \end{align}$$Moment of inertia
The moment of inertia about the CM of the cylinder is $$I_{cm}=\frac{1}{2}mr^2=\frac{1}{2}(1+u)m_0~(1+u)r_0^2=\frac{1}{2}(1+u)^2m_0r_0^2.$$ Angular momentum
The angular momentum of the cylinder has two parts, spin about the CM and orbital of the CM
(a) About the CM $$L_{spin}=I_{cm}\omega =I_{cm}\frac{v}{r}=\frac{1}{2}(1+u)^2m_0r_0^2\frac{v}{(1+u)^{1/2}r_0}=\frac{1}{2}(1+u)^{3/2}m_0vr_0.$$(b) Of the CM (orbital) $$L_{orb}=mvr=(1+u)^{3/2}m_0vr_0.$$The total angular momentum is $$L=L_{spin}+L_{orb}=\frac{3}{2}(1+u)^{3/2}m_0vr_0.$$Angular momentum is conserved as discussed above. $$0=\frac{dL}{dt}=v\frac{dL}{ds}=v\frac{\beta}{m_0}\frac{dL}{ds}=\frac{v\beta}{m_0} \frac{d}{du}\left(\frac{3}{2}(1+u)^{3/2}m_0vr_0\right).$$Dropping the irrelevant multiplicative parameters gives the ODE $$ \frac{d}{du}\left((1+u)^{3/2}v\right)=0\implies (1+u)^{3/2}v=const.$$ Answer
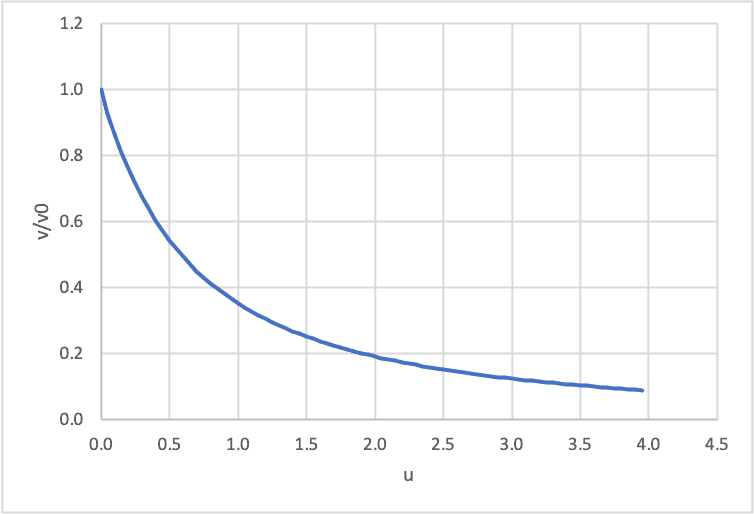
Since the initial speed is ##v_0##, we write $$v=\frac{v_0}{(1+u)^{3/2}}.$$A plot is shown below
Is mechanical energy conserved here?
The answer is no. A look at the speed verifies that. Here we have a deformable system in which one part of the system does work on the other. Any approach that relies on energy conservation must take that into account.
Edited to add the link to the other similar thread.
Here I will adopt a dynamic approach and consider that the angular momentum of the cylinder relative to the point of contact is conserved because the surface can exert no torque. For the reader's convenience, I reproduce derivations of relevant equations taken from the post quoted above.
Let ##\beta=## the rate at which the cylinder gathers snow. It is expedient to define dimensionless parameter ##u=\dfrac{\beta s}{m_0}## and write
Mass of cylinder: ##m=m_0+\beta s=(1+u)m_0.##
Radius of cylinder
To find ##r(s)## consider adding to the cylinder mass ##dm## in the form of a cylindrical tube of thickness ##dr## and radius ##r##. Then $$\begin{align} & \beta~ds=dm=\rho dV=\rho(2\pi r)(dr)L=\frac{m_0}{\pi r_0^2~L}(2\pi r)( dr)L=\frac{m_0}{ r_0^2}2rdr \nonumber \\
&\implies \frac{m_0}{ r_0^2} \int_{r_0}^{r}2rdr = \beta \int_0^s ds \implies r^2=r_0^2\left(1+\frac{\beta s}{m_0} \right)\implies r=(1+u)^{1/2}r_0.
\nonumber \end{align}$$Moment of inertia
The moment of inertia about the CM of the cylinder is $$I_{cm}=\frac{1}{2}mr^2=\frac{1}{2}(1+u)m_0~(1+u)r_0^2=\frac{1}{2}(1+u)^2m_0r_0^2.$$ Angular momentum
The angular momentum of the cylinder has two parts, spin about the CM and orbital of the CM
(a) About the CM $$L_{spin}=I_{cm}\omega =I_{cm}\frac{v}{r}=\frac{1}{2}(1+u)^2m_0r_0^2\frac{v}{(1+u)^{1/2}r_0}=\frac{1}{2}(1+u)^{3/2}m_0vr_0.$$(b) Of the CM (orbital) $$L_{orb}=mvr=(1+u)^{3/2}m_0vr_0.$$The total angular momentum is $$L=L_{spin}+L_{orb}=\frac{3}{2}(1+u)^{3/2}m_0vr_0.$$Angular momentum is conserved as discussed above. $$0=\frac{dL}{dt}=v\frac{dL}{ds}=v\frac{\beta}{m_0}\frac{dL}{ds}=\frac{v\beta}{m_0} \frac{d}{du}\left(\frac{3}{2}(1+u)^{3/2}m_0vr_0\right).$$Dropping the irrelevant multiplicative parameters gives the ODE $$ \frac{d}{du}\left((1+u)^{3/2}v\right)=0\implies (1+u)^{3/2}v=const.$$ Answer
Since the initial speed is ##v_0##, we write $$v=\frac{v_0}{(1+u)^{3/2}}.$$A plot is shown below
Is mechanical energy conserved here?
The answer is no. A look at the speed verifies that. Here we have a deformable system in which one part of the system does work on the other. Any approach that relies on energy conservation must take that into account.
Edited to add the link to the other similar thread.
Last edited: