MHB SW1986's question at Yahoo Answers regarding a solid of revolution

[MarkFL]

Here is the question:

Volume of a solid of revolution about x=3?

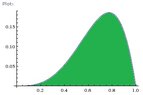
What is the volume of the solid of revolution bounded by
y=(x^3)-(x^5)
y=0
x=0
x=1

I have been using the shell method and I keep getting a negative answer which is obviously incorrect. (I keep getting 2pi(-14183/140). I'm trying to get the integral set up to use the washer method but I am having a very hard time integrating with respect to y instead of x. For example, I don't know how to express y=x^3-x^5 in terms of y. Help?

Here is a link to the question:

Volume of a solid of revolution about x=3? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Re: SW1986's question at Yahoo! Answers regarding a sold of revolution

Hello SW1986,

The first thing I like to do is plot the region to be revolved:

https://www.physicsforums.com/attachments/806._xfImport

Using the shell method, we may first compute the volume of an arbitrary shell:

$$dV=2\pi rh\,dx$$

where:

$$r=3-x$$

$$h=x^3-x^5$$

and so we have:

$$dV=2\pi (3-x)\left(x^3-x^5 \right)\,dx=2\pi\left(x^6-3x^5-x^4+3x^3 \right)\,dx$$

Summing the shells by integration, we then find:

$$V=2\pi\int_0^1 x^6-3x^5-x^4+3x^3\,dx=2\pi\left[\frac{x^7}{7}-\frac{x^6}{2}-\frac{x^5}{5}+\frac{3x^4}{4} \right]_0^1=2\pi\left(\frac{1}{7}-\frac{1}{2}-\frac{1}{5}+\frac{3}{4} \right)=\frac{27\pi}{70}$$

In this case, since we cannot explicitly solve the given function for $x$, using the washer method is impractical.

To SW1986 and any other guests viewing this topic, I invite and encourage you to post other calculus questions here in our http://www.mathhelpboards.com/f10/ forum.

Best Regards,

Mark.