Tension in legs of an insect dangling upside down

[coffeebird]

Homework Statement

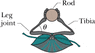
Some insects can walk below a thin rod (such as a twig) by hanging from it. Suppose that such an insect has mass m and hangs from a horizontal rod as shown in Fig. 5-35, with angle θ = 40°. Its six legs are all under the same tension, and the leg sections nearest the body are horizontal. (a) What is the ratio of the tension in each tibia (forepart of a leg) to the insect's weight? (b) If the insect straightens out its legs somewhat, does the tension in each tibia increase, decrease, or stay the same?

Homework Equations

F=ma

The Attempt at a Solution

weight = 9.8 m = tension on one leg = 9.8/6 m

tension in all tibias = (9.8mcos40)^2 + (9.8sin40)^2

tension in all femurs= 9.8cos40=7.51m

in answer to (b), the tension in the tibias would decrease because the tension in the femurs would increase

 

[TSny]

Hello, coffeebird.

weight = 9.8 m = tension on one leg = 9.8/6 m

Did you really want to claim that the weight of the bug equals the tension in one leg? Or, are you claiming that the tension in one leg equals 1/6 the weight of the bug? Either way, you would need to justify that.

It might help to relate this problem to the more standard problem of finding the tension in two cords that support a hanging sign, as shown in the attached figure. The key to working problems like this is to draw a good free-body diagram of the sign. Likewise, for the bug, draw a free-body diagram of the bug treating the tibias as "cords" supporting the bug.

 

[bigQ]

(a) There are six legs, and the vertical component of the tension force in each leg is
T sinθ where θ = 40° . For vertical equilibrium (zero acceleration in the y direction) then by
Newton’s second law
6T sinθ= mg
∴ T = mg/6 sinθ
∴ the ratio becomes T/mg ≈ 0.259
(b) The angle θ is measured from horizontal, so as the insect “straightens out the legs” θ
will increase (getting closer to 90° ), which causes sinθ to increase (getting closer to 1)
and consequently (since sinθ is in the denominator) causes T to decrease.

 

[coffeebird]

thank you, i get it now