Tension in the string while it descends

[Asterast]

Homework Statement

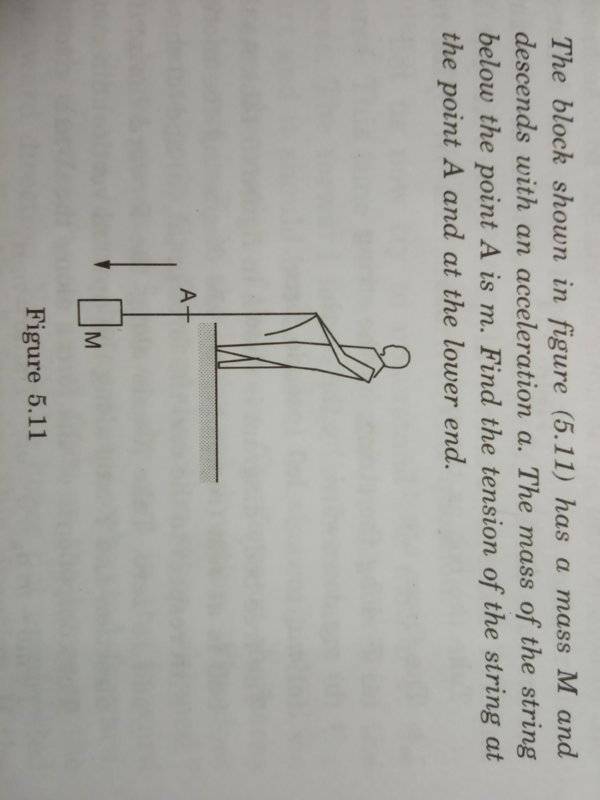
The block in figure has a mass M and descends with an acceleration a. The mass of the string below the point A is m. Find the tension of the string at the point A and at lower end.

Relevant Equations

Newton's laws of motion.

so I took string below point A and Block as a system. Taking mass of string below point A as m and mass of block M. Taking downward direction as X axis. I get Mg+mg-T, Taking T as tension by upward part of string. Now the question says about block descending with acceleration a.
so again forces acting on system will be (M+m)a since it is going down. Total sum of forces will be
(M+m)g-T+(M+m)a = 0, so tension at point A will be (M+m)(g+a) = T.
but answer is (M+m)(g-a) = T.
What is it that I'm doing wrong?

 

[BvU]

Hello Asterast, !

What is it that I'm doing wrong?

Well, for one thing, you are posting the picture sideways. That hurts my neck

$g$ and $a$ are vectors: they have a magnitude and a direction. The directions are opposite. In this case, 'up' was chosen as positive, so for $a$ the vertical component is negative: minus the magnitude.

 

[BvU]

Correction: you chose x+ is downwards

The force balance/Newtons's law for your system reads $$ (M+m)g + T = (M+m)a $$ with a positive value for g and $a$ positive value for $a$. So the tension force T on your 'system' is $$ (M+m) (g-a) = -T $$, i.e. for $|a| < |g|$ the tension T force on your system is upwards. The tension in the wire is |T|

 

[Asterast]

Correction: you chose x+ is downwards

The force balance/Newtons's law for your system reads $$ (M+m)g + T = (M+m)a $$ with a positive value for g and $a$ positive value for $a$. So the tension force T on your 'system' is $$ (M+m) (g-a) = -T $$, i.e. for $|a| < |g|$ the tension T force on your system is upwards. The tension in the wire is |T|

Consider me really dumb but how's the force of descent is equal to sum of forces due to tension and gravitation.
Sorry I'm new here, don't know how to rotate the image in the post.
Thank you for your time. :)

 

[jbriggs444]

Consider me really dumb but how's the force of descent is equal to sum of forces due to tension and gravitation.

Unless you are adopting the accelerating frame of reference in which the block and string are always at rest, there is no "force of descent" equal to (m+M)a involved here.

Cast the equation in the standard form: $\sum F=ma$ and adopt a consistent sign convention. The whole problem you are having is about sign conventions.

 

[BvU]

@Asterast : glad to see others agree:

Cast the equation in the standard form: $\sum F=ma$

As you can see from $$(M+m)g + T = (M+m)a $$ I've been conditioned to do just that

There are only two forces working on your system: gravity and Tension. Their resultant is responsible for the acceleration.

 

[brotherbobby]

Well, for one thing, you are posting the picture sideways. That hurts my neck

I agree. We must do a better job with pictures or diagrams and equations in this forum. I can suggest the students to use InkScape as an excellent software with LaTeX embedded so that we can draw as well as put equations into the drawings. Let us stop taking images from books when we can do a much better job of drawing them ourselves!

 

[Asterast]

@Asterast : glad to see others agree:
As you can see from $$(M+m)g + T = (M+m)a $$ I've been conditioned to do just that

There are only two forces working on your system: gravity and Tension. Their resultant is responsible for the acceleration.

Aye! I got it now. Thank you folks :)

 

[Asterast]

I agree. We must do a better job with pictures or diagrams and equations in this forum. I can suggest the students to use InkScape as an excellent software with LaTeX embedded so that we can draw as well as put equations into the drawings. Let us stop taking images from books when we can do a much better job of drawing them ourselves!

:) thanks I'll try this in future threads.