- #1
Elenor
- 4
- 0
1. Homework Statement :
A 4.00 kg object is attached to a vertical rod by two strings (as below). The object rotates in a horizontal circle at constant speed 6.00 m/s.
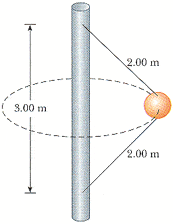
mass = 4.00 kg
V = 6.00 m/s
centripetal acceleration = Ac
Ac = V^2/r
[tex]
\vec{F}_{net} = \Sigma \vec{F} = m \vec{a}
[/tex]
mass = 4.00 kg
V = 6.00 m/s
Using trig, the radius (r) = 1.3229m
The lower angle of the top triangle (composed of the half the length of the rod, the length of the string, and the radius) should be 48.5904 degrees. The upper angle would then be 41.4096 degrees.
Using (Ac = V^2/r): (6.00m/s)^2/1.3229m = Ac = 27.2129m/s^2
T1 is the upper string, and
T2 in the lower string.
g = 9.8 m/(s^2)
Here is my main concern--do I have the following two equations right?
[tex]
(\vec{F}_{net})_x = \Sigma F_x = 0
[/tex] = m(Ac) - T1cos(41.4096) - T2cos(41.4096)
[tex]
(\vec{F}_{net})_x = \Sigma F_x = 0
[/tex] = T1sin(41.4096) - T2sin(41.4096) - mg
Therefore:
X direction: m(Ac) = T1cos(41.4096) + T2cos(41.4096)
and
Y direction: mg = T1sin(41.4096) - T2sin(41.4096)
At this point I have all the values except T1 and T2, so I can solve for them . . .
T1 = [m(Ac) - T2cos(41.4096)]/cos(41.4096)
mg = {[m(Ac) - T2cos(41.4096)]/cos(41.4096)} sin(41.4096) - T2sin(41.4096)
mg = m(Ac)[sin(41.4096)]/cos(41.4096) - T2sin(41.4096) - T2sin(41.4096)
-mg + m(Ac)[sin(41.4096)]/cos(41.4096) = T2[sin(41.4096) + sin(41.4096)]
{m(Ac) sin(41.4096)/cos(41.4096) - mg} / 2sin(41.4096)] = T2
T2 = 42.9353N
And . . . using that value of T2, T1 = 102.2001N
Now, I've resorted to working the problem with these numbers, as I have an answer to the problems with these numbers . . . and my problem is that this is not right, and I can't figure out where I went wrong.
With these numbers, I know that the correct answers are: T1 = 109N and T2 = 56.4N
When I figure out what I'm doing wrong, and how to do it right . . . I'll switch to the other set of numbers, for my problem.
Is my method correct? Frequently my problems are due to some little think like forgetting to square something . . . If that's all it is, I'm sorry to bother you guys with it. However, I'll be glad for any help you can give me with this problem! Thank you very much!
A 4.00 kg object is attached to a vertical rod by two strings (as below). The object rotates in a horizontal circle at constant speed 6.00 m/s.
mass = 4.00 kg
V = 6.00 m/s
Homework Equations
centripetal acceleration = Ac
Ac = V^2/r
[tex]
\vec{F}_{net} = \Sigma \vec{F} = m \vec{a}
[/tex]
The Attempt at a Solution
mass = 4.00 kg
V = 6.00 m/s
Using trig, the radius (r) = 1.3229m
The lower angle of the top triangle (composed of the half the length of the rod, the length of the string, and the radius) should be 48.5904 degrees. The upper angle would then be 41.4096 degrees.
Using (Ac = V^2/r): (6.00m/s)^2/1.3229m = Ac = 27.2129m/s^2
T1 is the upper string, and
T2 in the lower string.
g = 9.8 m/(s^2)
Here is my main concern--do I have the following two equations right?
[tex]
(\vec{F}_{net})_x = \Sigma F_x = 0
[/tex] = m(Ac) - T1cos(41.4096) - T2cos(41.4096)
[tex]
(\vec{F}_{net})_x = \Sigma F_x = 0
[/tex] = T1sin(41.4096) - T2sin(41.4096) - mg
Therefore:
X direction: m(Ac) = T1cos(41.4096) + T2cos(41.4096)
and
Y direction: mg = T1sin(41.4096) - T2sin(41.4096)
At this point I have all the values except T1 and T2, so I can solve for them . . .
T1 = [m(Ac) - T2cos(41.4096)]/cos(41.4096)
mg = {[m(Ac) - T2cos(41.4096)]/cos(41.4096)} sin(41.4096) - T2sin(41.4096)
mg = m(Ac)[sin(41.4096)]/cos(41.4096) - T2sin(41.4096) - T2sin(41.4096)
-mg + m(Ac)[sin(41.4096)]/cos(41.4096) = T2[sin(41.4096) + sin(41.4096)]
{m(Ac) sin(41.4096)/cos(41.4096) - mg} / 2sin(41.4096)] = T2
T2 = 42.9353N
And . . . using that value of T2, T1 = 102.2001N
Now, I've resorted to working the problem with these numbers, as I have an answer to the problems with these numbers . . . and my problem is that this is not right, and I can't figure out where I went wrong.
With these numbers, I know that the correct answers are: T1 = 109N and T2 = 56.4N
When I figure out what I'm doing wrong, and how to do it right . . . I'll switch to the other set of numbers, for my problem.
Is my method correct? Frequently my problems are due to some little think like forgetting to square something . . . If that's all it is, I'm sorry to bother you guys with it. However, I'll be glad for any help you can give me with this problem! Thank you very much!
Last edited: