The AM-GM Inequality - Sohrab Proposition 2.1.25 ....

[Math Amateur]

I am reading Houshang H. Sohrab's book: "Basic Real Analysis" (Second Edition).

I am focused on Chapter 2: Sequences and Series of Real Numbers ... ...

I need help with the proof of Proposition 2.1.25 ...

Proposition 2.1.25 reads as follows:

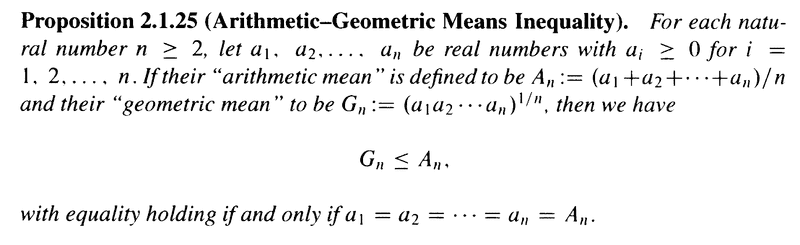
In the above proof, Sohrab appears to be using mathematical induction ... BUT ... he proves the inequality for $n= 2$, but then, in the inductive step, instead of assuming the inequality is true for $n$ and then proving it is true for $n+1$ ... Sohrab assumes the inequality is true for $n = 2^m$ and then proceeds to prove it true for $2n = 2^{ m+1}$ ... then finishes the proof by picking an $m$ such that $n \lt 2^m$ and establishing the inequality ...

My questions are as follows:

What is the valid proof process here ... ?

How does the proof process fit with the usual mathematical induction strategy ...Peter

 

[fresh_42]

The proof uses two principles of proofs:

1. Induction along $2^m$, i.e. he proves all cases $1,2,4,8,16, \ldots$, which results in a proven statement $\mathcal{A}$. It is the usual induction, since the steps are still by $1,2,3,4,5,\ldots$. The power is already part of the statement to be proven.
2. Direct proof. Here we assume an arbitrary, but fixed number $n$, where we may use $\mathcal{A}$ as a given, because proven statement. Since $n$ has been arbitrary, it holds unconditionally, i.e. for all $n \in \mathbb{N}$.

His last statement about the equality case is a bit confusing, because we don't need and extra induction. We can prove this case along the existing proof, because we only have one inequality in the last estimation which results from $\mathcal{A}$ and equality for arbitrary $n$ is the same as equality in $\mathcal{A}$, and this can be done within the first (inductive) part of the proof.

 

[Math Amateur]

Thanks fresh_42 ...

After reflecting on your statement ... it answers all my concerns ...

Thanks again,

Peter