The Calculus of folding to make boxes

[MarkFL]

Overview​

A common problem encountered by students in a first semester of elementary calculus involves taking a rectangular sheet of material and cutting squares from each corner so that, when the resulting flaps are folded upward, an open box is formed. The task is to determine the dimensions of the squares removed that maximize the volume of the box.

To analyze this problem in general terms, refer to the following diagram:

The width of the original sheet is labeled $W$ and the length is labeled $L$. The squares removed from each corner are shaded in black and have side length $x$.

---

Volume Function​

When the flaps are folded up, the base of the box has area

$$
A=(W-2x)(L-2x)
$$

and the height of the box is $x$. Therefore, the volume of the box as a function of $x$ is

$$
V(x)=x(W-2x)(L-2x)=4x^3-2(L+W)x^2+LWx
$$

---

Optimization​

Differentiating $V(x)$ with respect to $x$ and setting the result equal to zero yields

$$
V'(x)=12x^2-4(L+W)x+LW=0
$$

The derivative is a parabola opening upward, so the smaller of its two roots corresponds to a local maximum. Applying the quadratic formula, the maximizing value of $x$ is

$$
x=\frac{L+W-\sqrt{L^2-LW+W^2}}{6}
$$

---

Related Closed-Box Problem​

A related problem involves taking a rectangular sheet and removing congruent rectangles from two adjacent corners, leaving a shape that can be folded into a closed box.

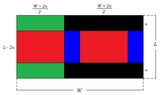
Refer to the following diagram:

The removed rectangles are shaded in black. The base and top of the resulting box are shaded in red, while the two pairs of opposing sides are shaded in green and blue.

The area of the base is

$$
b=\frac{1}{2}(W-2x)(L-2x)
$$

Since the height of the box is $x$, the volume is

$$
V(x)=bx=\frac{1}{2}(W-2x)(L-2x)x
$$

Recognizing that this volume function differs from the previous one only by a constant factor, we obtain the same critical value of $x$:

$$
x=\frac{L+W-\sqrt{L^2-LW+W^2}}{6}
$$

---

Dimensions of the Removed Rectangles​

The width of each removed rectangle is therefore

$$
w=\frac{W}{2}+x=\frac{L+4W-\sqrt{L^2-LW+W^2}}{6}
$$

 

[Greg Bernhardt]

Thanks @MarkFL! What math forum can we move this to?