- #1
Conn_coord
- 37
- 5
https://en.wikipedia.org/wiki/Wien's_displacement_law
Using the value 4 to solve the implicit equation yields the peak in the spectral radiance density function expressed in the parameter radiance per proportional bandwidth. (That is, the density of irradiance per frequency bandwidth proportional to the frequency itself, which can be calculated by taking considering infinitesimal intervals of {\displaystyle \ln \nu }
rather of frequency itself.) This is perhaps a more intuitive way of presenting "wavelength of peak emission". That yields x = 3.920690394872886343... to double precision floating point accuracy."
The CMB has a thermal black body spectrum at a temperature of 2.72548±0.00057 K
For example, using T = 2.725 K and parameterization by wavelength, the wavelength for maximal spectral radiance is λ = 1.063 mm with corresponding frequency ν = 282 GHz. For the same temperature, but parameterizing by frequency, the frequency for maximal spectral radiance is ν = 160,23 GHz with corresponding wavelength λ = 1.87 1 nm.
Parametrization by frequency
$$\nu_{peak} = \frac{xkT }{h}$$
$$x=2.821439372122078893$$
where x from $$(x-3)\cdot e^x +3 =0$$
Parametrization by wavelength
$$\lambda_{peak} = \frac{hc}{xkT }$$
$$x=4.965114231744276304$$
where x from $$(x-5)\cdot e^x + 5=0$$
And for "wavelength of peak emission"
$$ (x-4) \cdot e^x + 4=0 $$
$$ x = 4 +W(-4e^{-4}) $$
$$ x = 3.920690394872886343 $$
160.23Ghz / 2.82143937 * 3.920690 =222,65GHz or
c/222,65GHz = 1,35 mm
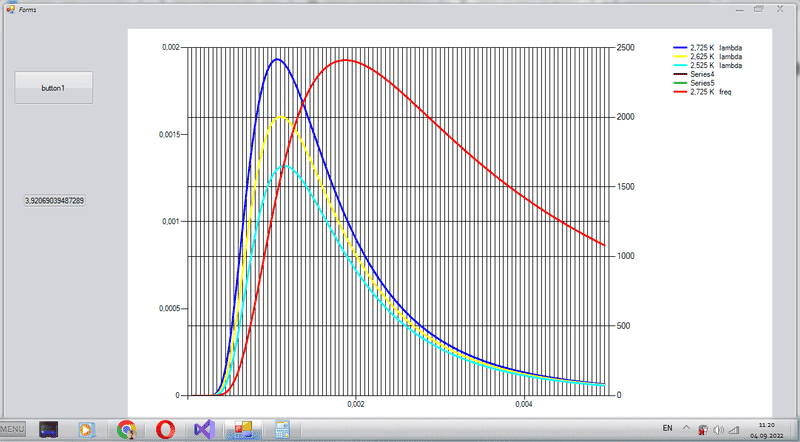
This is the intersection point of such graphs
parameterization by wavelength (blue)
parameterizing by frequency (red)
I also found another formula for CMB:
$$ \nu_{peak} = const \cdot H_o \cdot \sqrt{\alpha \cdot e^{\frac{1}{\alpha}}}$$
$$ H_0 \cdot \sqrt{\alpha \cdot e^{\frac{1}{\alpha}}} \approx 106 GHz$$
Planck 2018 results. VI. Cosmological parameters Planck Collaboration // Astronomy and Astrophysics.
"Maxima differ according to parameterization
...Using the value 4 to solve the implicit equation yields the peak in the spectral radiance density function expressed in the parameter radiance per proportional bandwidth. (That is, the density of irradiance per frequency bandwidth proportional to the frequency itself, which can be calculated by taking considering infinitesimal intervals of {\displaystyle \ln \nu }
The CMB has a thermal black body spectrum at a temperature of 2.72548±0.00057 K
For example, using T = 2.725 K and parameterization by wavelength, the wavelength for maximal spectral radiance is λ = 1.063 mm with corresponding frequency ν = 282 GHz. For the same temperature, but parameterizing by frequency, the frequency for maximal spectral radiance is ν = 160,23 GHz with corresponding wavelength λ = 1.87 1 nm.
Parametrization by frequency
$$\nu_{peak} = \frac{xkT }{h}$$
$$x=2.821439372122078893$$
where x from $$(x-3)\cdot e^x +3 =0$$
Parametrization by wavelength
$$\lambda_{peak} = \frac{hc}{xkT }$$
$$x=4.965114231744276304$$
where x from $$(x-5)\cdot e^x + 5=0$$
And for "wavelength of peak emission"
$$ (x-4) \cdot e^x + 4=0 $$
$$ x = 4 +W(-4e^{-4}) $$
$$ x = 3.920690394872886343 $$
160.23Ghz / 2.82143937 * 3.920690 =222,65GHz or
c/222,65GHz = 1,35 mm
This is the intersection point of such graphs
parameterization by wavelength (blue)
parameterizing by frequency (red)
I also found another formula for CMB:
$$ \nu_{peak} = const \cdot H_o \cdot \sqrt{\alpha \cdot e^{\frac{1}{\alpha}}}$$
$$ H_0 \cdot \sqrt{\alpha \cdot e^{\frac{1}{\alpha}}} \approx 106 GHz$$
Planck 2018 results. VI. Cosmological parameters Planck Collaboration // Astronomy and Astrophysics.
Last edited:
